Mensaje de error

  • Deprecated function: The each() function is deprecated. This message will be suppressed on further calls en book_prev() (línea 775 de /home1/montes/public_html/drupal/modules/book/book.module).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Deprecated function: implode(): Passing glue string after array is deprecated. Swap the parameters en drupal_get_feeds() (línea 394 de /home1/montes/public_html/drupal/includes/common.inc).

Ejercicio 3.7(b) Momento dipolar, coordenadas esfericas, coordenadas cartesianas

Solapas principales

Enviado por Anónimo (no verificado) en Mié, 12/04/2013 - 18:32
[adsense:336x280:9156825571]

Resolucion:

El momento dipolar de coordenadas cartesianas a coordenadas esfericas:

\begin{bmatrix}mdp_{r} \\ mdp_{\theta} \\ mdp_{\phi} \\ \end{bmatrix}= =\begin{bmatrix}sen(\theta)\cdot cos(\phi) & sen(\theta)\cdot sen(\phi) & cos(\theta) \\ cos(\theta)\cdot cos(\phi) & cos(\theta)\cdot sen(\phi) & -sen(\theta) \\ -sen(\phi) & cos(\phi) & 0 \end{bmatrix} \cdot \cdot\begin{bmatrix}mdp_{x} \\ mdp_{y} \\ mdp_{z} \\ \end{bmatrix}=\begin{bmatrix}sen(\theta)\cdot cos(\phi) & sen(\theta)\cdot sen(\phi) & cos(\theta) \\ cos(\theta)\cdot cos(\phi) & cos(\theta)\cdot sen(\phi) & -sen(\theta) \\ -sen(\phi) & cos(\phi) & 0 \end{bmatrix} \cdot \begin{bmatrix}0 \\ 0 \\ 0.1\cdot 10^{-9} \\ \end{bmatrix}=\begin{bmatrix}1\cdot 10^{-9}\cdot cos(\theta) \\ 1\cdot 10^{-9}\cdot -sen(\theta) \\ 0 \\ \end{bmatrix}

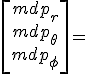
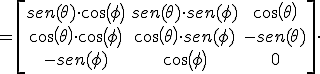
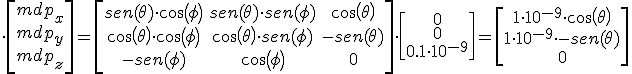
El potencial electrico dado el momento dipolar en el punto en coordenadas esfericas.

V=\frac{\bar{mdp}\cdot \bar{a_{r}}}{4\cdot \pi \epsilon_{o}\cdot r^2}=\frac{0.1\cdot 10^{-9}\cdot 9\cdot 10^{9}\cdot cos(\frac{\pi}{3})}{ 2^2}=0.1125\,V

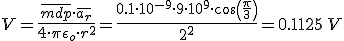
El campo electrico dado el momento dipolar en el punto en coordenadas esfericas.

E=-\nabla\,V=\frac{\partial{V}}{\partial{r}}\cdot \bar{a}_{r}+\frac{1}{r}\cdot \frac{\partial{V}}{\partial{\theta}}\cdot \bar{a}_{\theta}+\frac{1}{r\cdot sen(\theta)}\cdot \frac{\partial{V}}{\partial{\phi}}\cdot \bar{a}_{\phi}= -\frac{\partial{\frac{0.9\cdot cos(\theta)}{r^2}}}{\partial{r}}\cdot \bar{a}_{r}-\frac{1}{r}\cdot \frac{\partial{\frac{0.9\cdot cos(\theta)}{r^2}}}{\partial{\theta}}\cdot \bar{a}_{\theta}-\frac{1}{r\cdot sen(\theta)}\cdot \frac{\partial{\frac{0.9\cdot cos(\theta)}{r^2}}}{\partial{\phi}}\cdot \bar{a}_{\phi}= =2\cdot \frac{0.9\cdot cos(\theta)}{r^3}\cdot \bar{a}_{r}+\frac{1}{r}\cdot \frac{0.9\cdot sen(\theta)}{r^2}\cdot \bar{a}_{\theta}+0=2\cdot \frac{0.9\cdot cos(\frac{\pi}{3})}{2^3}\cdot \bar{a}_{r}+\frac{1}{2}\cdot \frac{0.9\cdot sen(\frac{\pi}{3})}{2^2}\cdot \bar{a}_{\theta}=0.1125\cdot \bar{a}_{r}+0.097\cdot \bar{a}_{\theta}

Tags:

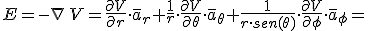
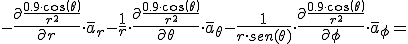
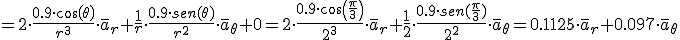
Español

Añadir nuevo comentario

Más información sobre los formatos de texto

Plain text

  • No se permiten etiquetas HTML.
  • Las direcciones de las páginas web y las de correo se convierten en enlaces automáticamente.
  • Saltos automáticos de líneas y de párrafos.
Pin It