Mensaje de error

Deprecated function: implode(): Passing glue string after array is deprecated. Swap the parameters en drupal_get_feeds() (línea 394 de /home1/montes/public_html/drupal/includes/common.inc).

step

Undefined

Programa 5.6 pag 252, Ogata

Vamos a calcular el tiempo de subid, tiempo de pico, maxima sobreelongacion y tiempo de asentamiento utilizando el Scilab del siguiente sistema:

 

Funcion de transferencia de segundo orden, Transformada de Laplace


Programa en Scilab: 
num=poly([25 0 0],'s','coeff');

den=poly([25 6 1],'s','coeff');

t=0:0.005:5;

g=syslin('c',num/den);

gs=csim('step',t,g);

r=1;

while gs(r)<1.0001;

r=r+1;

end;
tiemposubida=(r-1)*0.005;

[gsmax,rp]=max(gs);

tiempopico=(rp-1)*0.005;

ElongacionMax=gsmax-1;

rmax=5/0.005;

k=rmax+1;

while gs(k)>0.98 & gs(k)<1.02;
k=k-1;
end;

-->tiemposubida
 tiemposubida  =
 
    0.555  
 
-->tiempopico
 tiempopico  =
 
    0.785  
 
-->ElongacionMax
 ElongacionMax  =
 
    0.0947800  
 
-->tiempoasentamiento
 tiempoasentamiento  =
 
    1.185

 

Español

Programa 5.5 pag 250, Ogata

[adsense:336x280:9156825571]
Vamos a hacer la representacion grafica de la respuesta a una entrada escalon unitario, dando a el factor
de amortiguacion los siguientes valores del sistema:$\zeta=0, 0.2, 0.4, 0.6, 0.8, 1.0 $
Funcion de tranferencia con el factor de amortiguacion, Transformada de Laplace

 

Programa en Scilab:
t=0:0.2:10;

zeta=[0 0.2 0.4 0.6 0.8 1];

cv=[1 2 3 4 5 6];

for n=1:6

num=poly([1 0 0],'s','coeff');

den=poly([1 2*zeta(n) 1],'s','coeff');

g=syslin('c',num/den);

gs=csim('step',t,g);

plot2d(t,gs,style=cv(n))

end;

xgrid;

xtitle('Representacion a un escalon unitario con wn=1,zeta=0 , 0.2
, 0.4,0.6,0.8,1','t(seg)','Respuesta');

legends(['zeta=0','zeta=0.2','zeta=0.4','zeta=0.6','zeta=0.8','zeta=1']
,[1,2,3,4,5,6],opt=4);
Respuesta del sistema a un escalor para varios valores del factor de amortiguamiento con Scilab

 

Español

Programa 5.4 pag 250, Ogata

[adsense:336x280:9156825571]
Vamos a hacer la representacion grafica de la respuesta a una entrada escalon unitario del sistema:

 

Funcion de transferencia del sistema de segundo orden, Transformada de Laplace
Programa en Scilab:
num=poly([25 0 0 ],'s','coeff');

den=poly([25 4 1],'s','coeff');

g=syslin('c',num/den);

t=0:0.005:3;

gs=csim('step',t,g);

plot2d(t,gs);

xgrid;

xtitle('Respuesta a un escalon unitario G(s)=25/(s^2+4s+25)','Tiempo(seg)'
,'Amplitud')

Respuesta del sistema a un escalon unitario con Scilab

 

Español

Respuesta Transitoria

 

Español

Programa 7.5 OGATA 4edicion pag455

Vamos a dibujar la respuesta a un escalon para los valores de $K=0.4490$ y $K=1.4130$ mediante el Scilab del sistema en lazo cerrado:

 

Funcion de transferencia en lazo cerrado, transformada de Laplace


Programa en Scilab:
s=%s;

k1=0.4490;

g1=20/(s*(s+1)*(s+4)+20*(1+k1*s));

k2=1.4130;

g2=20/(s*(s+1)*(s+4)+20*(1+k2*s));

t=0:0.1:10;

y1=csim('step',t,g1);

y2=csim('step',t,g2);

clf;

plot(t,y1,'k');

plot(t,y2,'b');

xgrid;

xtitle('Respuesta a un escalon unitario de un sistema paralelo','t','salida');

legend(['K=0.4490';'K=1.4130'],style=4);
Respuesta del sistema a un escalon para dos valores de ganancia con Scilab
Español

Ejemplo 7.3 OGATA 4edicion pag444

Vamos a calcular el lugar de las raices mediante Scilab de un sistema en lazo cerrado con realimentación unitaria cuyo funcion de transferencia en lazo abierto es:Vamos a solucionar el problema del libro de otra forma. La funcion de transferencia en lazo abierto es:

 

Funcion de transferencia del sistema en lazo abierto


 

  1. Calculamos el polo dominante
    Tenemos el factor amortiguamient de 0.5 y la frecuencia natural no amortiguada 5. Por lo tanto el polo dominante tiene que estar en:

     

    polo dominante


     

  2. Calculamos el angulo a corregir:

     

    Valor de la funcion de transferencia para el polo dominante

     

     

    angulo a corregir

     

     

    180-angulo a corregir


     

     

    representacion de los angulos

 

 

 

  1. Calculamos $T_{1}$ y $\gamma$

    compensador para corregir el angulo


    Vamos a posicionar el cero en -2.5 .Alineado con el polo dominante.

     

    posicion de los polos y ceros del compensador

     

     

    distancia entre polos


     

    distancia entre el polo y el cero


     

    funcion de transferencia del compensador de adelanto


     

    Tenemos un cero en -2.5 y un polo en -8.63. Por lo tanto el compensador adelanto queda:

     

    \begin{displaymath}K_{c}\cdot \frac{s+\frac{1}{T_{1}}}{s+\frac{\gamma}{T_{1}}}=K_{c}\cdot \frac{s+2.5}{s+8.63} \end{displaymath}


     

    Por lo que podemos calcular el valor de $\gamma$

     

    ecuaciones para calcular la gamma

     

    valor de la gamma


     

  2. Vamos a calcular el valor de $K_{c}$

     

    ecuacion del valor de la ganancia del compensador de adelanto

     

     

    valor de la ganancia del compensador de adelanto


     

    Con lo que el compensador de adelanto queda:

     

    Funcion de transferencia del compensador de adelanto


     

  3. Vamos a calcular el $\beta$ del compensador de atraso. Sabiendo que $Kv=80$

     

    funcion de transferencia del compensador de atraso

     

    ganancia del compensador de atraso

     

     

    valor de la beta

     

  4. Escogiendo $T_{2}=5$ como en el libro vamos a comprobar que verifica las condiciones el compensador

     

    funcion de transferencia obtenida para el compensador de atraso


     

    valor del compensador de atraso para el polo dominante

     

    angulo del compensador de atraso para el polo dominante

     

     

    \begin{displaymath}-5º<-1.42<0º\end{displaymath}


     

    Con lo que verifica las condiciones. El compensador adelanto-atraso nos quedaria:

     

    Funcion de transferencia para el compensador adelanto atraso


     

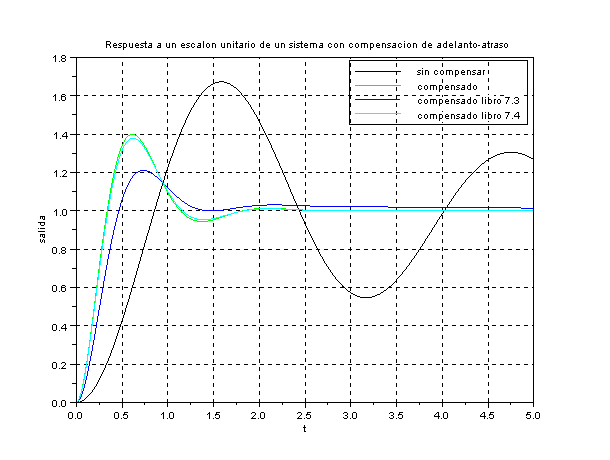
Vamos a sacar las graficas de respuesta del sistema(el que calculamos,el del libro y el del ejemplo 7.4 del libro) a una entrada escalon . Tambien se mostrara la programacion de todos los calculos obtenidos.

Programa en Scilab:
s=%s;
g=4/(s*(s+0.5));
s1=-2.5+5*sqrt(1-0.5^2)*%i;
gs=syslin('c',g);
gs1=horner(gs,s1);
angulo=180-360*atan(abs(imag(gs1))/abs(real(gs1)))/(2*%pi);
angulocorregir=180-angulo;
l=imag(s1)*tan(2*%pi*angulocorregir/360);
p1=-2.5-l;
z1=-2.5;
gc=(s-z1)/(s-p1);
gma=p1/z1;
gt=gc*g;
aux1=(abs(horner(gt,s1)));
kc=1/aux1;
gct=kc*gc;
gt2=kc*gt;
aux3=s*gt2;
aux4=horner(aux3,0);
b=80/aux4;
gc2=(s+(1/5))/(s+(1/(5*b)));
aux5=horner(gc2,s1);
aux6=abs(aux5);
angulo2=-360*atan(abs(imag(aux5))/abs(real(aux5)))/(2*%pi);
gt3=gc2*gt2;
gct2=6.26*((s+0.5)/(s+5.02))*((s+0.2)/(s+0.01247));
gt4=g*gct2;
gct3=10*((s+2.38)/(s+8.34))*((s+0.1)/(s+0.0285));
gt5=g*gct3;
t=0:0.01:5;
glc=g /. 1;
glc1=gt3 /. 1;
glc2=gt4 /. 1;
glc3=gt5 /. 1;
y=csim('step',t,glc);
y1=csim('step',t,glc1);
y2=csim('step',t,glc2);
y3=csim('step',t,glc3);
clf;
//negro sistema sin compensar
plot(t,y,'k');
//verde, sistema compensado que se ha calculado
plot(t,y1,'g');
//azul,sistema compensado del libro ejemplo 7.3
plot(t,y2,'b');
//cyan sistema compensado del libro ejemplo 7.4
plot(t,y3,'c');

legend(['sin compensar';'compensado';'compensado libro 7.3';'compensado 
libro 7.4']);

xtitle('Respuesta a un escalon unitario de un sistema con compensacion de 
adelanto-atraso','t','salida');

xgrid;
respuesta del sistema compensado y no compensado a un impulso con Scilab

Ahora vamos a dibujar la respuesta a una rampa.

 

Añadimo al programa anterior en Scilab el siguiente codigo:
y=csim(t,t,glc);
y1=csim(t,t,glc1);
y2=csim(t,t,glc2);
y3=csim(t,t,glc3);
clf;
plot(t,t,'r');
//negro sistema sin compensar
plot(t,y,'k');
//verde, sistema compensado que se ha calculado
plot(t,y1,'g');
//azul,sistema compensado del libro ejemplo 7.3
plot(t,y2,'b');
//cyan sistema compensado del libro ejemplo 7.4
plot(t,y3,'c');

legend(['rampa';'sin compensar';'compensado';'compensado libro 7.3';'compensado
 libro 7.4'],style=4);

xtitle('Respuesta a una rampa unitaria de un sistema con compensacion de 
adelanto-atraso','t','salida');

xgrid;
respuesta del sistema compensado y no compensado a una rampa con Scilab
Español

Programa 7.4 OGATA 4edicion pag438

Vamos a dibujar la respuesta a una rampa mediante el Scilab de un sistema compensado y no compensado. El sistema en lazo abierto a compensar es el siguiente:

 

Funcion de transferencia del sistema en lazo abierto sin compensar


 

El sistema de compensacion (compensador de adelanto) obtenido es:

 

Funcion de transferencia del compensador de atraso

 

 

Programa en Scilab:
clf;

s=%s;

g=1.06/(s*(s+1)*(s+2));

gc=0.9656*(s+0.05)/(s+0.005);

gt=gc*g;

gc=g /. 1;

gct=gt /. 1;

t=0:0.1:50;

gs=syslin('c',gc);

gcs=syslin('c',gct);

y=csim('step',t,gs);

yt=csim('step',t,gcs);

plot(t,y);

plot(t,yt,'g');

xgrid;

xtitle('Respuesta a un escalon unitario de un sistema con compensacion de atraso'
,'t','salida');

legend(['no compensado';'compensado'],style=4);

 

Respuesta del sistema compensado y no compensado a una entrada escalon con Scilab
Español

Programa 7.1 OGATA 4edicion pag428

Vamos a dibujar mediante el Scilab un sistema compensado y no compensado a una entrada escalon. El sistema en lazo abierto a compensar es el siguinte:

 

Funcion de transferencia en lazo abierto, Transformada de Laplace


 

El sistema de compensacion (compensador de adelanto) obtenido es:

 

Compensador de adelanto del sistema


Programa en Scilab:
clf;
 
s=%s;
 
g=4/(s*(s+2));
 
gs=4.68*(s+2.9)/(s+5.4);
 
gc=g/. 1;
 
gt=gs*g;
 
gtc=gt/. 1;
 
t=0:0.05:5;
 
gcs=syslin('c',gc);
 
gtcs=syslin('c',gtc);
 
y=csim('step',t,gcs);
 
yt=csim('step',t,gtcs);
 
plot(t,y);
 
plot(t,yt,'g');
 
xgrid;
 
legend(['no compensado';'compensado'],style=4);
Salida del sistema compensado y no compensado a una entrada escalon con Scilab
Español

Páginas
Pin It
Subscribe to RSS - step