Mensaje de error

  • Deprecated function: The each() function is deprecated. This message will be suppressed on further calls en book_prev() (línea 775 de /home1/montes/public_html/drupal/modules/book/book.module).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Deprecated function: implode(): Passing glue string after array is deprecated. Swap the parameters en drupal_get_feeds() (línea 394 de /home1/montes/public_html/drupal/includes/common.inc).

Apartada a) de la cuestion 2 EDiferenciales 1209S1 (Wronskiano)

Solapas principales

Enviado por Anónimo (no verificado) en Mar, 06/03/2014 - 10:55
[adsense:336x280:9156825571]

a) Resolucion:

Vamos a calcular el Wronskonsiano de las dos soluciones de la ecuacion diferencial:
 
W=\begin{vmatrix} e^x & x\cdot e^x \\ e^x & e^x+x\cdot e^x \\ \end{vmatrix}=
=e^{2\cdot x}+x\cdot e^{2\cdot x}-x\cdot e^{2\cdot x}=
=e^{2\cdot x}\neq 0 \hspace{0,2cm}\text{Para x distinto de cero}
 
 
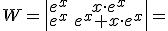
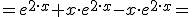
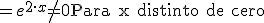
Para que las soluciones sean linealmente dependientes en un intervalo el wronskiano debe ser cero en el intervalo. Como se ve W es distinto de cero lo que implica que las soluciones son linealmente independientes. En el punto 0  el W vale cero pero para ser dependientes tendria que valer cero en todo el intervalos, es decir para todo valor de x.
 
 
Programa en Sagemath para calcular el wronskiano de dos soluciones de la ecuacion diferencial.
Sage: var('x')
Sage: r=wronskian(e^(x),x*e^(x))
Sage: r.expand()

Resultado de la wronskiano con Sage 
e^(2*x)
 

 

Tags:

Español
google+: 
View profile on Google+

Añadir nuevo comentario

Más información sobre los formatos de texto

Plain text

  • No se permiten etiquetas HTML.
  • Las direcciones de las páginas web y las de correo se convierten en enlaces automáticamente.
  • Saltos automáticos de líneas y de párrafos.
Pin It