[adsense:responsibe:9545213979]
Problema A.5.24 pag 323, Ogata
Solapas principales
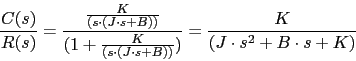
![]()
![]()
Ante una entrada rampa
![]() obtenemos que la Transformda de Laplace del error es:
obtenemos que la Transformda de Laplace del error es:
![]()
El error e(t) en el infinito sera utilizando el Teorema del valor final:
![]()
Si aumentamos K para eliminar el error, el valor de
![]() disminuira con lo que se aumenta la sobreelongacion.
disminuira con lo que se aumenta la sobreelongacion.
Para corregir esto tenemos dos soluciones:
a)Utilizar un control proporcional derivativo
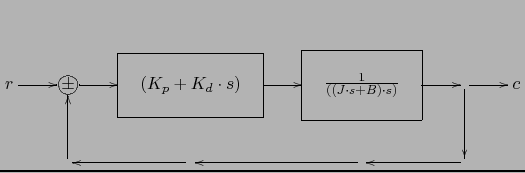
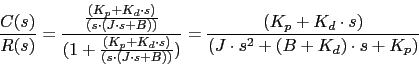
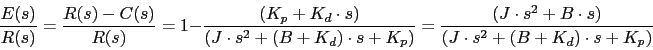
Ante una entrada rampa
![]() obtenemos que la Transformda de Laplace del error es:
obtenemos que la Transformda de Laplace del error es:
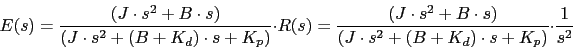
El error e(t) en el infinito sera utilizando el Teorema del valor final:
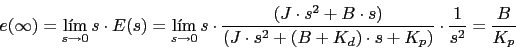
El error vale igual lo que cambia es el valor de
![]() con lo que aunque aumentemos
con lo que aunque aumentemos ![]() para eliminar el error, podemos aumentar
para eliminar el error, podemos aumentar ![]() para que el valor de
para que el valor de ![]() no disminuya.
no disminuya.
b)Utilizar un servosistema con realimentación de velocidad:
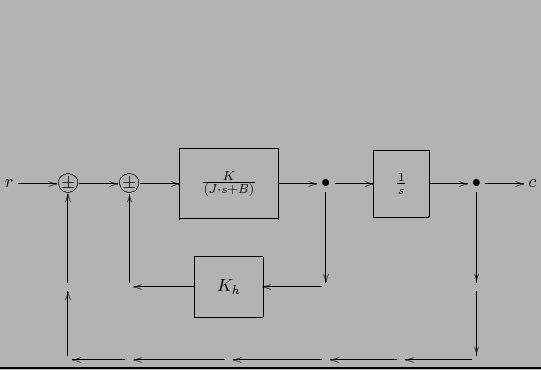
Calculamos la función de transferencia del lazo interior
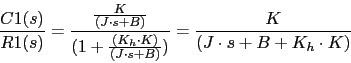
Calculamo la función de transferencia de todo el sistema
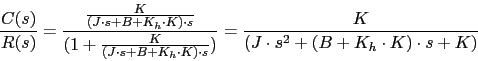
![]()
Ante una entrada rampa
![]() obtenemos que la Transformda de Laplace del error es:
obtenemos que la Transformda de Laplace del error es:
![]()
El error e(t) en el infinito sera utilizando el Teorema del valor final:
![]()
Si aumentamos K para que el error valga casi cero, el factor de amortiguamiento
![]() no tiende hacia cero, con lo que tendriamos una sobreelongacion elevada, debido a
no tiende hacia cero, con lo que tendriamos una sobreelongacion elevada, debido a ![]()



Añadir nuevo comentario