[adsense:responsibe:9545213979]
Ejercicio 3.12 Condiciones frontera dielectricos
Solapas principales
[adsense:336x280:9156825571]
Resolucion:
Si es isotropo su susceptibilidad es un escalar:
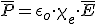
Como es homogeneo la polaridad es homogeneo la permitividad es un escalar, es decir es uniforme:
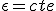
Suponemos que no hay carga libre en la superficie frontera con lo que la densidad de carga superficial sera cero.
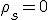
Para el encontrar la intensidad de campo en el dielectrico 2, utilizaremos las condiciones de frontera:
Componentes tangenciales: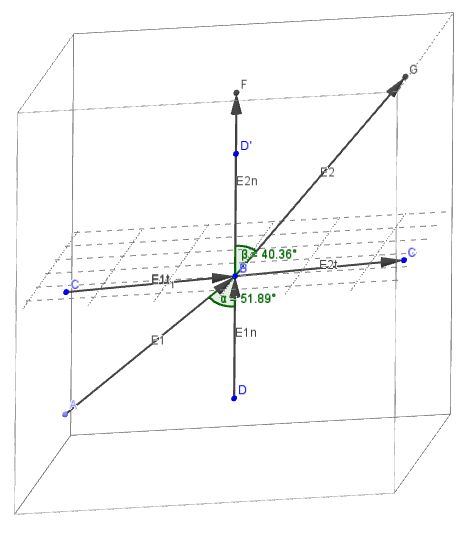
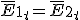
Como el plano es el plano xy
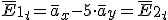
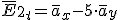
Componentes normales:
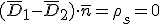
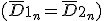
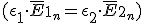
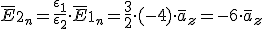
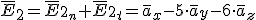
El angulo que formo la intensidad de campo primera con la normal a la superficie viene dado por:
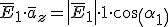
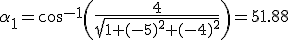
El angulo que formo la intensidad de campo primera con la normal a la superficie viene dado por:
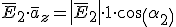
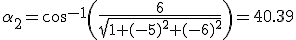
Español



Añadir nuevo comentario