Vamos a calcular las transformada de Laplace de las funciones siguientes.
a)
Solucion:
Vamos a utilizar las siguientes propiedades y tranformadas.
Con lo que obtenemos:
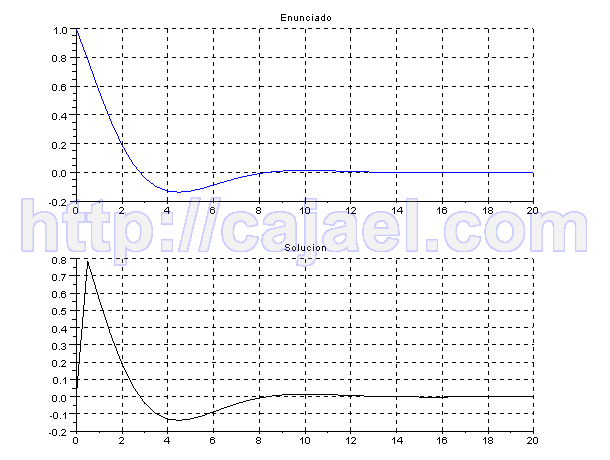
Vamos a comprobar el resultado con el Scilab.
t=0:0.5:20;
ft=exp(-0.4*t).*cos(12*t);
s=%s;
numfs=s+0.4;
denfs=(s+0.4)^2+12^2;
fs=syslin('c',numfs/denfs);
fs1=csim('impulse',t,fs);
subplot(2,1,1);
plot2d(t,ft,2);
xtitle('Enunciado');
xgrid;
subplot(2,1,2);
plot2d(t,fs1,1);
xtitle('Solucion');
xgrid;
[adsense:336x280:9156825571]
b)
Solucion:
Vamos a descomponer la funcion de la siguiente manera:
Con lo que la transformada nos quedaria:
Vamos a comprobar el resultado con el Scilab.
t=0:0.5:300;
ft=sin(4*t+(%pi/3));
s=%s;
fs=(4/(s^2+4^2))*cos(%pi/3)+(s/(s^2+4^2))*sin(%pi/3);
fs2=syslin('c',fs);
fs1=csim('impulse',t,fs2);
subplot(2,1,1);
plot2d(t,ft,2);
xtitle('Enunciado');
xgrid;
subplot(2,1,2);
plot2d(t,fs1,1);
xtitle('Solucion');
xgrid;
Comentarios recientes