Vamos a hacer la representacion grafica de la solucion del Ejemplo 5.9 que viene dada por una entrada escalon unitario al sistema(programado en Scilab):
Programa en Scilab:
num=poly([0 0.35 0.1],'s','coeff');
den=poly([2 3 1],'s','coeff');
t=0:0.1:7;
g=syslin('c',num/den);
gs=csim('step',t,g);
plot(t,gs);
xgrid;
xtitle('respuesta a un Escalon unitario de G(s)=(0.1s^2+0.35s)/(s^2+3s+2)'
,'t(seg)','Amplitud')
Como se ve la funcion sale del 0 cuando tendria que salir del 0.1 vamos a repetir el programa pero utilizando en vez de una entrada escalon para
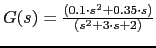 , una entrada impulso para el sistema
, una entrada impulso para el sistema
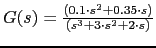 , es decir, lo mismo. Si nos fijamos al ejecutar el codigo anterior de Scilab, el sistema nos da un warning despues de ejecutar el csim.
, es decir, lo mismo. Si nos fijamos al ejecutar el codigo anterior de Scilab, el sistema nos da un warning despues de ejecutar el csim.
Programa en Scilab:
num=poly([0 0.35 0.1 0],'s','coeff');
den=poly([0 2 3 1],'s','coeff');
t=0:0.1:7;
g=syslin('c',num/den);
gs=csim('impulse',t,g);
plot2d(t,gs,2);
xgrid;
xtitle('respuesta a un impulso unitario de G(s)=(0.1s^2+0.35s)/(s^3+3s^2+2s)'
,'t(seg)','Amplitud');
Comentarios recientes