Mensaje de error

  • Deprecated function: The each() function is deprecated. This message will be suppressed on further calls en book_prev() (línea 775 de /home1/montes/public_html/drupal/modules/book/book.module).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Deprecated function: implode(): Passing glue string after array is deprecated. Swap the parameters en drupal_get_feeds() (línea 394 de /home1/montes/public_html/drupal/includes/common.inc).

Apartada b.1) de la cuestion 3 EDiferenciales 1406S2 (Sistema ecuaciones diferenciales; Solucion general): Page 2 of 3

Solapas principales

Enviado por Anónimo (no verificado) en Jue, 06/26/2014 - 18:19
[adsense:336x280:9156825571]
Con lo que tenemos un vector propio por ejemplo:
 
\begin{pmatrix} u_1 \\ u_2 \\ \end{pmatrix}= \begin{pmatrix} 1 \\ 0 \\ \end{pmatrix}
 
\begin{pmatrix} 0 & 2 \\ 0 & 0 \\ \end{pmatrix}\cdot \begin{pmatrix} v_1 \\ v_2 \\ \end{pmatrix}=\begin{pmatrix} u_1 \\ u_2 \\ \end{pmatrix}
 
2\cdot v_2=u_1
v_{2}=\frac{u_1}{2}=\frac{1}{2}
 
\begin{pmatrix} v_1 \\ v_2 \\ \end{pmatrix}= \begin{pmatrix} v_1 \\ \frac{1}{2} \\ \end{pmatrix}= \begin{pmatrix} 1 \\ \frac{1}{2} \\ \end{pmatrix}
X_1=\begin{pmatrix} 1 \\ 0 \\ \end{pmatrix} \cdot e^{1\cdot t}
X_2=\begin{pmatrix} 1 \\ 0 \\ \end{pmatrix}\cdot t \cdot e^{1\cdot t}+\begin{pmatrix} 1 \\ \frac{1}{2} \\ \end{pmatrix}\cdot e^{1\cdot t}
 
 
X_1=\begin{pmatrix} e^{ t} \\ 0 \\ \end{pmatrix}
X_2=\begin{pmatrix} t \cdot e^{ t}+ e^{ t} \\ \frac{e^{ t}}{2} \\ \end{pmatrix}
 
 
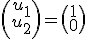
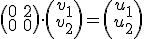
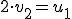
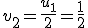
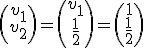
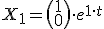
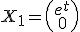
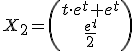
Programa en Sagemath para comprobar los valores propios de la ecuacion diferencial
Sage: var('al k')
Sage: var('u1 u2')
Sage: A = matrix([[1, 2], [0, 1]])
Sage: B=matrix.identity(2)
Sage: C=A-(1)*B
Sage: E=matrix([[1],[0]])
Sage: F=matrix([[v1],[v2]])
Sage: G=C*F-E
Sage: A.eigenspaces_right(),G
Resultado con Sagemath del vectores propios
(
[      
(1, Vector space of degree 2 and dimension 1 over Rational Field
User basis matrix:                                              
[1 0])                                                          
]    
[2*v2 - 1]
[       0]
)

Tags:

Español
google+: 
View profile on Google+

Páginas

Añadir nuevo comentario

Más información sobre los formatos de texto

Plain text

  • No se permiten etiquetas HTML.
  • Las direcciones de las páginas web y las de correo se convierten en enlaces automáticamente.
  • Saltos automáticos de líneas y de párrafos.
Pin It