[adsense:responsibe:9545213979]
Ejercicio 4.14 Hambley (polarizacion automatica, linea de carga)
Solapas principales
a)
![]()
![]()
![]()
Los puntos de corte con los ejes de la linea de carga del transistor en ![]()
![]()
![]()
Los puntos de corte con los ejes de la linea de carga del transistor en ![]()
![]()
![]()
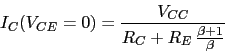
![]()
Si aumenta un poco ![]() , el punto
, el punto
![]() disminuye un poco lo que implica que la linea de carga del transistor baja un poco. Pero la
disminuye un poco lo que implica que la linea de carga del transistor baja un poco. Pero la ![]() no se desplaza debido a que vale
no se desplaza debido a que vale
![]() .
.
b)
Los puntos de corte con los ejes de la linea de carga del transistor en ![]()
![]()
![]()
Los puntos de corte con los ejes de la linea de carga del transistor en ![]()
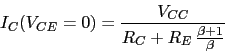
![]()
Si aumenta un poco ![]() , el punto
, el punto
![]() disminuye lo que implica que la linea de carga del transistor baja en
disminuye lo que implica que la linea de carga del transistor baja en ![]() . Con lo que la
. Con lo que la ![]() se desplaza hacia abajo.
se desplaza hacia abajo.
Si aumenta un poco ![]() , el punto
, el punto
![]() disminuye un poco lo que implica que la linea de carga del transistor baja un poco. Como la
disminuye un poco lo que implica que la linea de carga del transistor baja un poco. Como la ![]() ha disminuido, la linea a cortar
ha disminuido, la linea a cortar ![]() por la linea de carga del transistor en
por la linea de carga del transistor en ![]() esta mas baja. Debido a esto, la
esta mas baja. Debido a esto, la ![]() estara mas abajo lo que implica que disminuira .
estara mas abajo lo que implica que disminuira .
c)
![]()
![]()
Los puntos de corte con los ejes de la linea de carga del transistor en ![]()
![]()
![]()
Los puntos de corte con los ejes de la linea de carga del transistor en ![]()
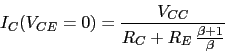
![]()
Si aumenta un poco ![]() , aumenta
, aumenta ![]() y disminuye
y disminuye ![]() , con lo que los puntos
, con lo que los puntos
![]() y
y
![]() disminuyen lo que implica que la linea de carga del transistor baja en
disminuyen lo que implica que la linea de carga del transistor baja en ![]() . Con lo que la
. Con lo que la ![]() se desplaza hacia abajo. Como la
se desplaza hacia abajo. Como la ![]() ha disminuido, la linea a cortar
ha disminuido, la linea a cortar ![]() por la linea de carga del transistor en
por la linea de carga del transistor en ![]() esta mas baja. Debido a esto, la
esta mas baja. Debido a esto, la ![]() estara mas abajo lo que implica que disminuye de valor .
estara mas abajo lo que implica que disminuye de valor .
d)
![]()
![]()
Los puntos de corte con los ejes de la linea de carga del transistor en ![]()
![]()
![]()
Los puntos de corte con los ejes de la linea de carga del transistor en ![]()
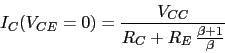
![]()
Si aumenta un poco ![]() , aumenta
, aumenta ![]() y aumenta
y aumenta ![]() , con lo que
, con lo que
![]() aumenta, lo que implica que la linea de carga del transistor sube en
aumenta, lo que implica que la linea de carga del transistor sube en ![]() . Con lo que la
. Con lo que la ![]() se desplaza hacia arriba. Como la
se desplaza hacia arriba. Como la ![]() ha aumentado, la linea a cortar
ha aumentado, la linea a cortar ![]() por la linea de carga del transistor en
por la linea de carga del transistor en ![]() esta mas alta. Debido a esto, la
esta mas alta. Debido a esto, la ![]() estara mas arriba lo que implica que aumenta de valor .
estara mas arriba lo que implica que aumenta de valor .
e)
Los puntos de corte con los ejes de la linea de carga del transistor en ![]()
![]()
![]()
Los puntos de corte con los ejes de la linea de carga del transistor en ![]()
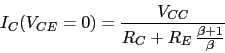
![]()
Si aumenta un poco ![]() , el punto
, el punto
![]() aumenta un poco lo que implica que la linea de carga del transistor aumenta un poco. Como la
aumenta un poco lo que implica que la linea de carga del transistor aumenta un poco. Como la ![]() ha aumentado, la linea a cortar
ha aumentado, la linea a cortar ![]() por la linea de carga del transistor en
por la linea de carga del transistor en ![]() esta mas alta. Debido a estos hechos, la
esta mas alta. Debido a estos hechos, la ![]() estara mas arriba lo que implica que aumentara.
estara mas arriba lo que implica que aumentara.



Añadir nuevo comentario