[adsense:responsibe:9545213979]
Resumen de tipos de Ecuaciones Diferenciales
Solapas principales
[adsense:336x280:9156825571]
Resumen de tipos de Ecuaciones Diferenciales:
Ecuacion diferencial de variables separables de primer orden::
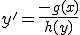
Ecuacion diferencial homogenea de grado m de primer orden::
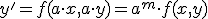
Ecuacion diferencial exacta de primer orden:
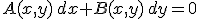
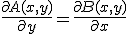
Ecuacion diferencial exacta con factor integrante u de primer orden:
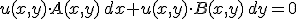
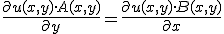
Ecuacion diferencial lineal de primer orden:
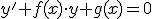
Ecuacion de diferencial de Bernuilli
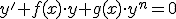
Ecuacion de diferencial de Riccati
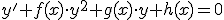
Ecuaciones forma:
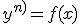
Ecuaciones diferenciales sin variable independiente:
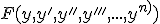
Ecuaciones diferenciales que no contienen a la funcion ni a sus derivadas hasta un orden:
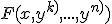
Ecuaciones diferenciales homogeneas respecto a la funcion y sus derivadas:
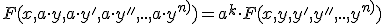
Ecuaciones diferenciales que son derivadas de otra expresion:
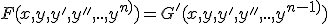
Español



Añadir nuevo comentario