[adsense:responsibe:9545213979]
Problema A9.9 pag667 OGATA
Solapas principales
Vamos a calcularle un compensador de retardo-adelanto que nos haga cumplir los siguientes requisitos 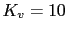 , margen de fase =50 y margen de ganancia
, margen de fase =50 y margen de ganancia 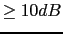 al siguiente sistema en lazo abierto:
al siguiente sistema en lazo abierto:
![]()
-
Vamos a calcular primero el valor de K para obtener
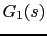
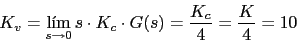
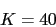
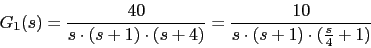
-
Vamos a calcular el diagrama de Bode de
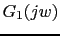
w 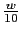
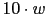
s 1 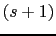
1 0.1 10 (s+4) 4 0.4 40 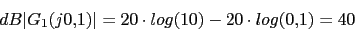
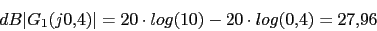
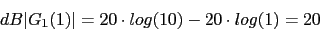
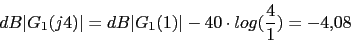
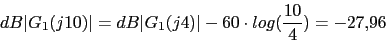
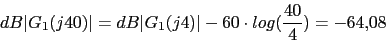
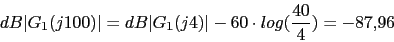
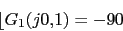
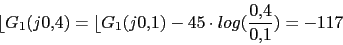
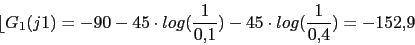
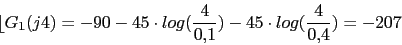
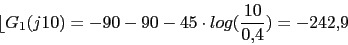
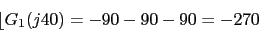
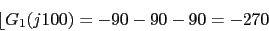
w 0.1 0.4 1 4 10 40 100 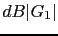
40 27.96 20 -4.08 -27.96 -64.08 -87.96 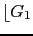
-90 -117 -152.9 -207 -242.9 -270 -270 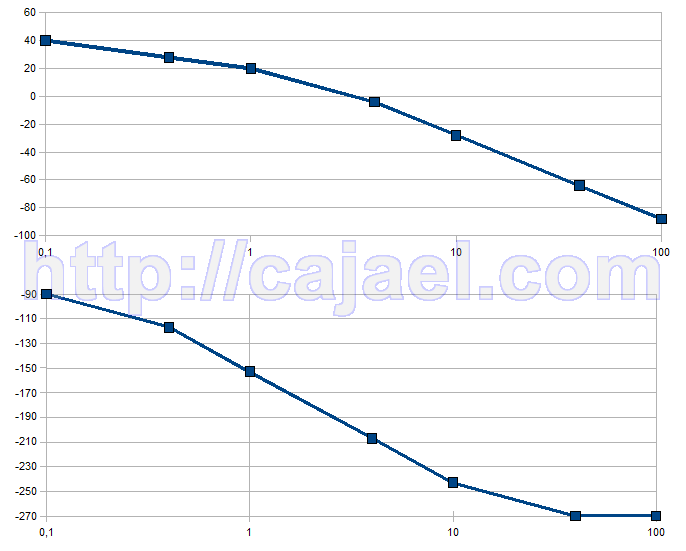
-
Vamos a calcular la frecuencia a la cual
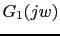 toma el valor -180, que sera la nueva frecuencia de cruce
toma el valor -180, que sera la nueva frecuencia de cruce
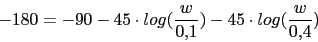
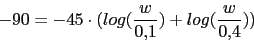
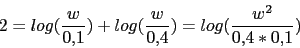
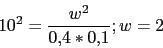 Comprobacion con Scilab
Comprobacion con Scilabs=%s; g=40/(s*(s+1)*(s+4)); gs=syslin('c',g); w=[0.1 0.4 1 2 4 10 40 100]; gr=horner(gs,%i*w); [phi,db]=phasemag(gr) [w;db;phi]Resultados:-->[w;db;phi] ans = 0.1 0.4 1. 2. 4. 39.954073 27.271007 16.726411 6.0205999 - 7.355989 - 97.142689 - 117.512 - 149.03624 - 180. - 210.96376 10. 40. 100. - 28.646594 - 64.128327 - 87.966178 - 242.488 - 262.85731 - 267.13645 -
El valor
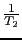 del compensador de atraso sera una decada por debajo de la frecuencia de cruce
del compensador de atraso sera una decada por debajo de la frecuencia de cruce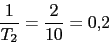
-
El margen de fase tendra que ser
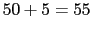 , con lo que con este valor calcularemos la
, con lo que con este valor calcularemos la 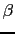
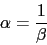
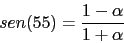
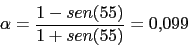
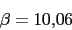 Con lo que ya tendremos el compensador de atraso
Con lo que ya tendremos el compensador de atraso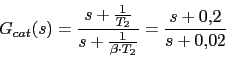 Vamos a representar el diagrama de Bode con el compensador mediante Scilab
Vamos a representar el diagrama de Bode con el compensador mediante Scilabs=%s/(2*%pi); g=40/(s*(s+1)*(s+4)); gc1=(s+0.2)/(s+0.02); gt1=g*gc1; gs=syslin('c',g); gc1s=syslin('c',gc1); gt1s=syslin('c',gt1); clf(); bode([gs;gt1s;gc1s],['compensador';'compensado';'no compensado']);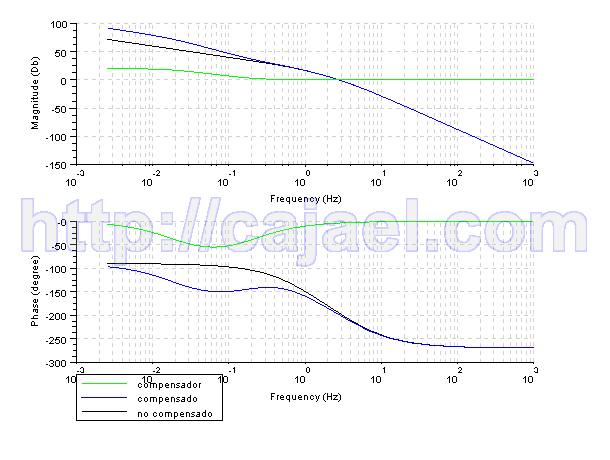
-
Vamos a calcular el compensador de adelanto. Vamos a calcular la ganancia que toma
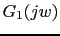 en la frecuencia de cruce:
en la frecuencia de cruce:
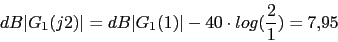 Vamos a calcular el cero y el polo del compensador pasando una recta por el punto (2rad/seg,-7.95dB) del diagrama de Bode y viendo donde interseca con la recta -20dB y la recta 0db. La pendiente viene dada de la siguiente forma:
Vamos a calcular el cero y el polo del compensador pasando una recta por el punto (2rad/seg,-7.95dB) del diagrama de Bode y viendo donde interseca con la recta -20dB y la recta 0db. La pendiente viene dada de la siguiente forma:
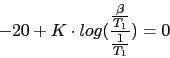
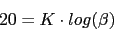
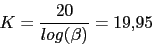
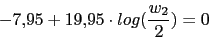
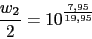
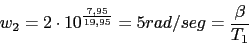
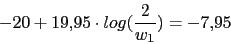
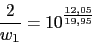
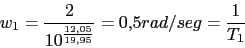 El compensador de adelanto nos quedara:
El compensador de adelanto nos quedara: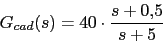
Vamos a representar el diagrama de Bode con el compensador mediante Scilab
s=%s/(2*%pi);
g=40/(s*(s+1)*(s+4));
gc1=(s+0.2)/(s+0.02);
gc2=(s+0.5)/(s+5);
gc3=(s+0.4)*(s+0.2)/((s+4)*(s+0.02));
gt1=g*gc1*gc2;
gt2=gc3*g;
gs=syslin('c',g);
gc1s=syslin('c',gc1*gc2);
gc2s=syslin('c',gc3);
gt1s=syslin('c',gt1);
gt2s=syslin('c',gt2);
clf();
bode([gs;gt1s;gc1s;gc2s;gt2s],['compensado libro';'compensador libro'
;'compensador';'compensado';'no compensado']);
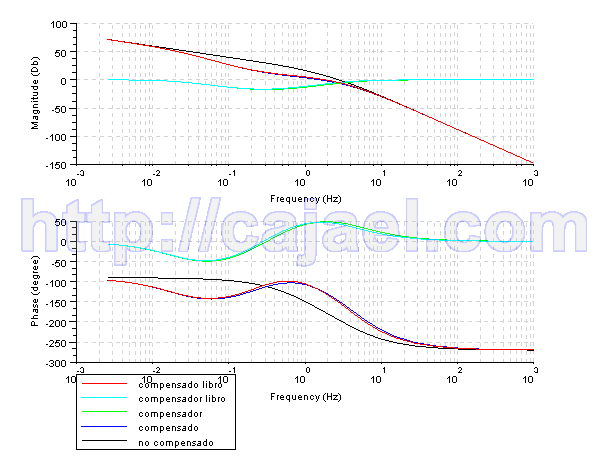
Si ampliamos el grafico, vemos que el margen de ganancia es mayor que 10dB

Vamos a ver la respuesta ante una entrada escalon del sistema mediante Scilab
s=%s;
g=40/(s*(s+1)*(s+4));
gc1=(s+0.2)/(s+0.02);
gc2=(s+0.5)/(s+5);
gc3=(s+0.4)*(s+0.2)/((s+4)*(s+0.02));
gt1=g*gc1*gc2;
gt2=gc3*g;
glc=g /. 1;
glc2=gt1 /. 1;
glc3=gt2 /. 1;
gs=syslin('c',glc);
gs2=syslin('c',glc2);
gs3=syslin('c',glc3);
t=0:0.1:40;
y=csim('step',t,gs);
y2=csim('step',t,gs2);
y3=csim('step',t,gs3);
clf();
subplot(2,1,1);
plot(t,y,1);
legends('no compensado',1,opt=1)
xgrid;
xtitle('Respuesta ante una entrada escalon','','y(t)')
subplot(2,1,2)
plot(t,y2,'b');
plot(t,y3,'g');
legends(['compensado';'compensado libro'],[2;3],opt=4);
xtitle('','t(seg)','y(t)')
xgrid;
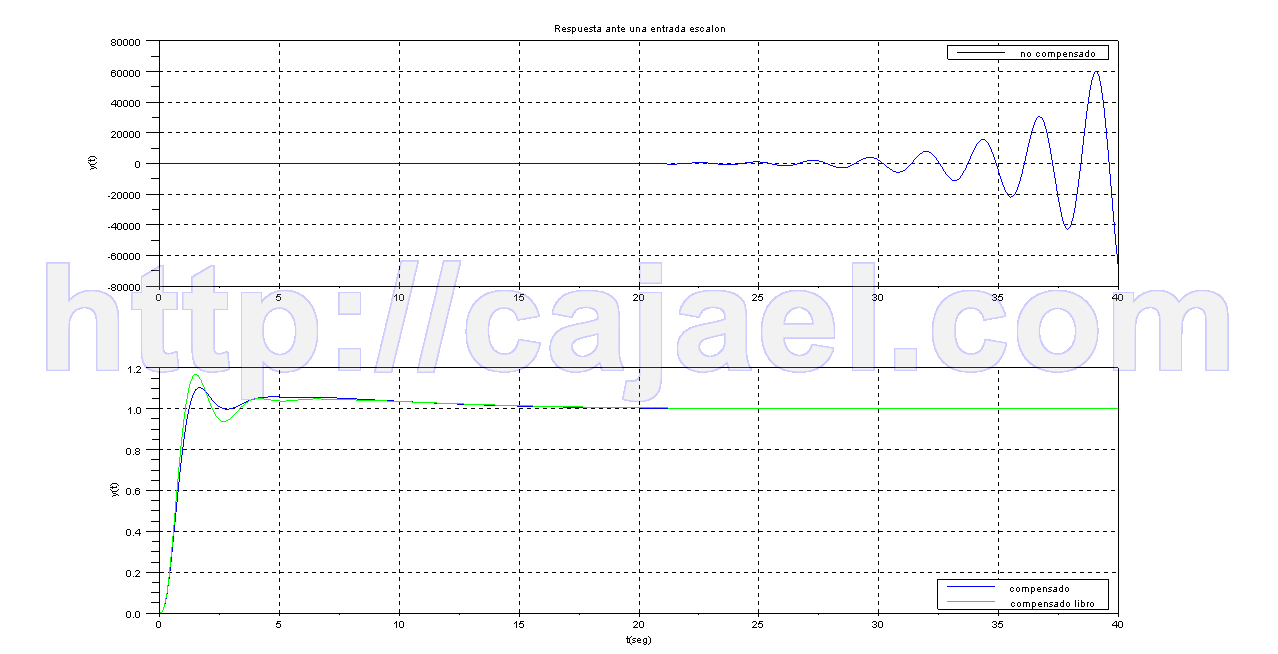
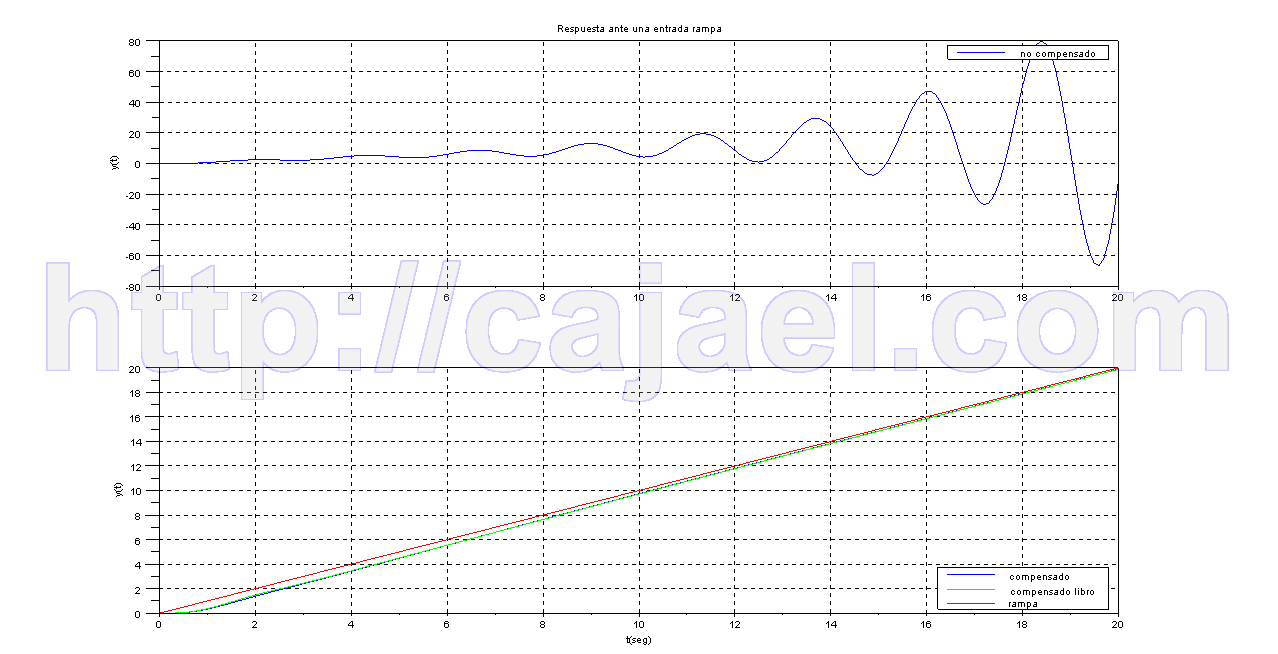
Vamos a ver la respuesta ante una rampa del sistema mediante Scilab
s=%s;
g=40/(s*(s+1)*(s+4));
gc1=(s+0.2)/(s+0.02);
gc2=(s+0.5)/(s+5);
gc3=(s+0.4)*(s+0.2)/((s+4)*(s+0.02));
gt1=g*gc1*gc2;
gt2=gc3*g;
glc=g /. 1;
glc2=gt1 /. 1;
glc3=gt2 /. 1;
gs=syslin('c',glc);
gs2=syslin('c',glc2);
gs3=syslin('c',glc3);
t=0:0.1:20;
y=csim(t,t,gs);
y2=csim(t,t,gs2);
y3=csim(t,t,gs3);
clf();
subplot(2,1,1);
plot(t,y,1);
legends('no compensado',2,opt=1)
xgrid;
xtitle('Respuesta ante una entrada rampa','','y(t)')
subplot(2,1,2)
plot(t,t,'r');
plot(t,y2,'b');
plot(t,y3,'g');
legends(['compensado';'compensado libro';'rampa'],[2;3;5],opt=4);
xtitle('','t(seg)','y(t)')
xgrid;
Español



Añadir nuevo comentario