[adsense:responsibe:9545213979]
Problema A9.8 pag660 OGATA
Solapas principales
Vamos a calcularle un compensador que nos haga cumplir los siguientes requisitos 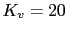 , margen de fase =50 y margen de ganancia
, margen de fase =50 y margen de ganancia 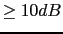 al siguiente sistema en lazo abierto:
al siguiente sistema en lazo abierto:
![]()
-
Vamos a calcular K y
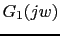
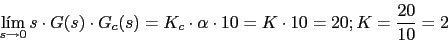
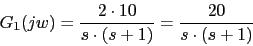
-
Vamos a hacer el diagrama de bode de
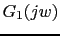
w 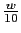
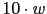
s 1 0.1 10 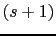
1 0.1 10 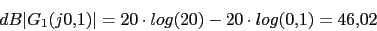
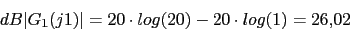
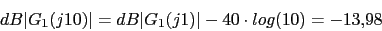
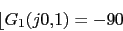
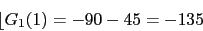
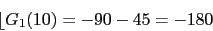
w 0.1 1 10 
46.02 26.02 -13.98 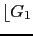
-90 -135 -180 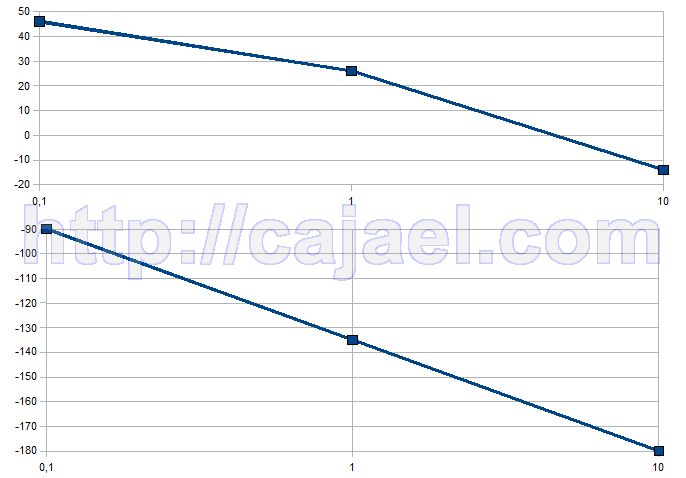
-
Como se ve necesitamos un compensador de adelanto para que el margen de fase sea 50
-
Vamos a calcular el margen de fase y la fase del compensador (
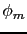 )
)
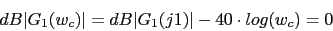
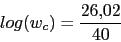
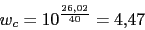
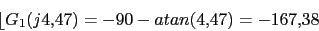
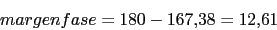
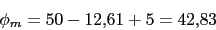
-
Calculamos el
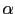 del compensador
del compensador
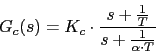
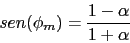
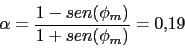
-
Calculamos el T del compensador
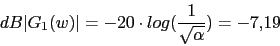
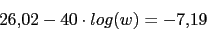
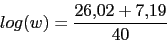
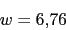 Este valor 6.76 sera la nueva frecuencia de corte.
Este valor 6.76 sera la nueva frecuencia de corte.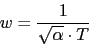
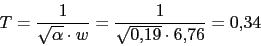
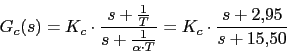
-
Calculamos la
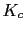 del compensador
del compensador
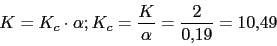 Con lo que el compensador nos queda:
Con lo que el compensador nos queda: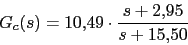
-
Ahora vamos a comprobar el margen de ganancia verifica
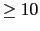 Al haber insertado en el sistema con el compensador un cero y polo, sus fases a altas frecuencias se anulan (90-90) con lo que el sistema queda como al inicio -180 a altas frecuencias casi en el
Al haber insertado en el sistema con el compensador un cero y polo, sus fases a altas frecuencias se anulan (90-90) con lo que el sistema queda como al inicio -180 a altas frecuencias casi en el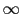 con lo que el margen de ganancia va ha ser muy elevado con lo que
con lo que el margen de ganancia va ha ser muy elevado con lo que 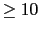 .
.
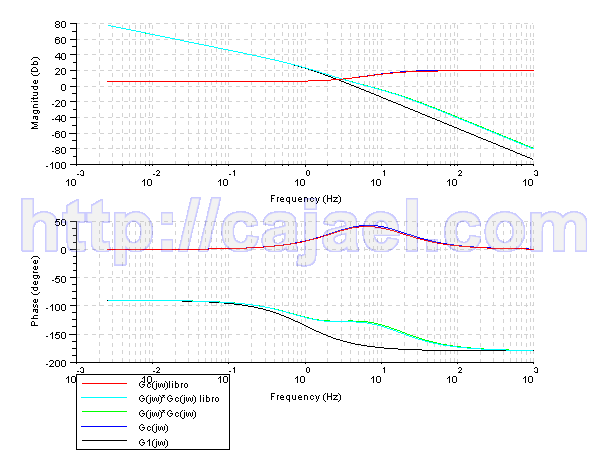
Vamos a representar el diagrama de Bode de todas las funciones mediante Scilab
s=%s/(2*%pi);
g=10/(s*(s+1))
gc=10.49*(s+2.95)/(s+15.5);
gt=g*gc;
gc2=9.5238*(s+2.9787)/(s+14.1842);
gt2=g*gc2;
gs=syslin('c',2*g);
gcs=syslin('c',gc);
gcs2=syslin('c',gc2);
gts=syslin('c',gt);
gts2=syslin('c',gt2);
clf();
bode([gs;gcs;gts;gts2;gcs2],['Gc(jw)libro';'G(jw)*Gc(jw)libro';'G(jw)
*Gc(jw)';'Gc(jw)';'G1(jw)' ]);
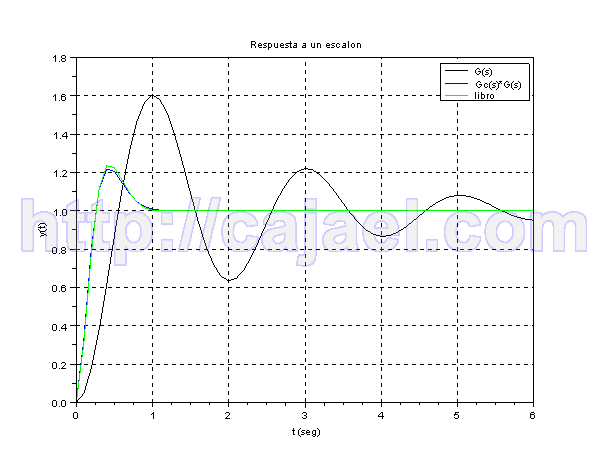
Vamos a representar la respuesta a un escalon mediante Scilab
s=%s;
g=10/(s*(s+1))
gc=10.49*(s+2.95)/(s+15.5);
gt=g*gc;
gc2=9.5238*(s+2.9787)/(s+14.1842);
gt2=g*gc2;
glc=g /. 1;
gtlc=gt /. 1;
gtlc2=gt2 /. 1;
gs=syslin('c',glc);
gcs=syslin('c',gtlc);
gcs2=syslin('c',gtlc2);
t=0:0.1:6;
y=csim('step',t,gs);
y1=csim('step',t,gcs);
y2=csim('step',t,gcs2);
clf();
plot(t,y,'k');
plot(t,y1,'b');
plot(t,y2,'g');
xtitle('Respuesta a un escalon','t (seg)','y(t)');
legends(['G(s)';'Gc(s)*G(s)';'libro'],[1,2,3],opt=1);
xgrid;
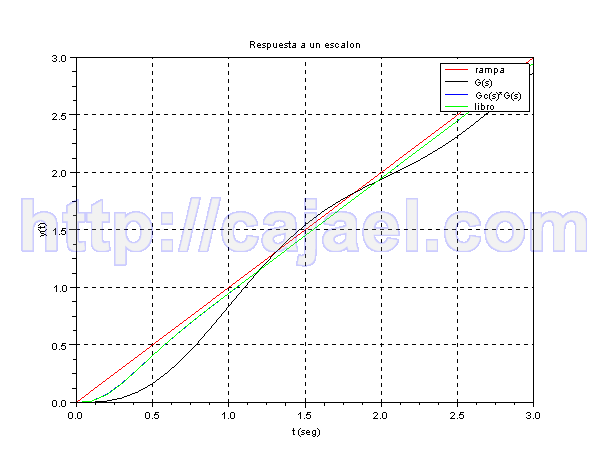
Vamos a representar la respuesta a una rampa mediante Scilab
s=%s;
g=10/(s*(s+1))
gc=10.49*(s+2.95)/(s+15.5);
gt=g*gc;
gc2=9.5238*(s+2.9787)/(s+14.1842);
gt2=g*gc2;
glc=g /. 1;
gtlc=gt /. 1;
gtlc2=gt2 /. 1;
gs=syslin('c',glc);
gcs=syslin('c',gtlc);
gcs2=syslin('c',gtlc2);
t=0:0.1:3;
y=csim(t,t,gs);
y1=csim(t,t,gcs);
y2=csim(t,t,gcs2);
clf();
plot(t,t,'r');
plot(t,y,'k');
plot(t,y1,'b');
plot(t,y2,'g');
xtitle('Respuesta a una rampa','t (seg)','y(t)');
legends(['rampa';'G(s)';'Gc(s)*G(s)';'libro'],[color('red'),1,2,3],opt=1);
xgrid;
Español



Añadir nuevo comentario