[adsense:responsibe:9545213979]
Problema A9.3 pag650 OGATA
Solapas principales
Sabiendo que queremos que el margen de fase se 60 grados. Vamos a determinar K.
![]()
SOLUCION
![]()
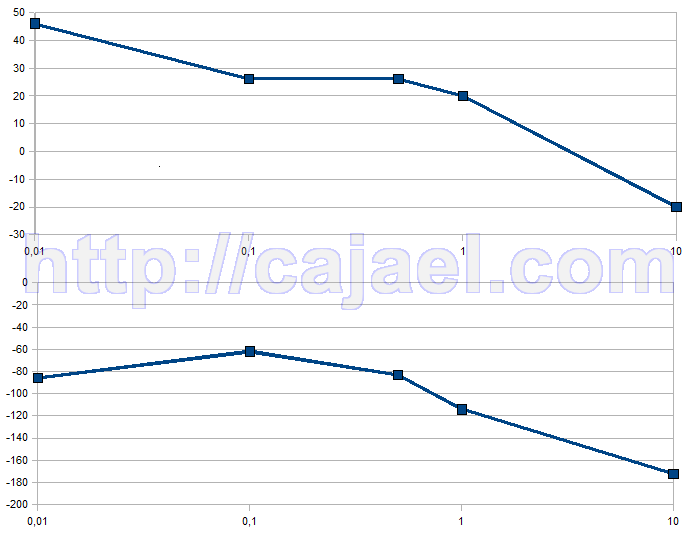
Vamos calcular el diagrama de bode del sistema.
| w | |
|
|
0.1 |
|
|
0.5 |
| s | 1 |
|
|
1 |
Vamos a calcular las ganancias para estas frecuencias de
![]()
![]()
![]()
![]()
![]()
![]()
| w | 0.01 | 0.1 | 0.5 | 1 | 10 |
|
|
46.02 | 26.02 | 26.02 | 20 | -20 |
|
|
-86 | -62 | -83 | -114 | -172 |
Vamos a calcular la fase a la cual se produce ese margen de fase:
![]()
Cuando la fase de la funcion 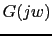 es igual a -120, esa frecuencia es la nueva frecuencia de cruce de ganancia.
es igual a -120, esa frecuencia es la nueva frecuencia de cruce de ganancia.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ahora vamos a calcular 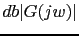 en la nueva frecuencia de corte.
en la nueva frecuencia de corte.
![]()
Con este valor calculamos el valor de K:
![]()
![]()
Comprobacion con Scilab
s=%s;
g=10*(s+0.1)/((s+0.5)*s*(s+1));
gs=syslin('c',g);
w=[0.01 0.1 0.5 1 1.1387 10];
gr=horner(gs,%i*w);
[phi,db]=phasemag(gr)
[w;db;phi]
Resultados:
-->[w;db;phi]
ans =
0.01 0.1 0.5 1. 1.1387
10.
46.061643 28.817353 22.211533 16.063814 14.528555
- 20.053623
- 86.008108 - 62.020526 - 82.874984 - 114.14554 - 120.02324
- 171.99994
Como se ve existe un pequeño error en la ganancia por la aproximancion.
![]()
![]()
Diagrama de bode en lazo abierto mediante Scilab.
s=%s/(2*%pi);
g=10*(s+0.1)/((s+0.5)*s*(s+1));
gs=syslin('c',0.13*g);
gs2=syslin('c',0.188*g);
clf;
bode([gs;gs2],['libro';'calculado']);
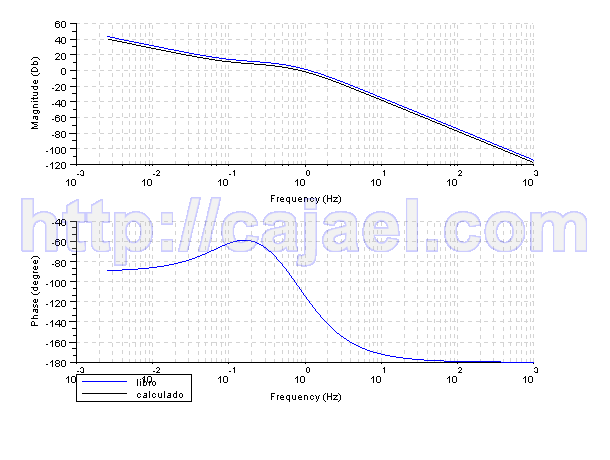
Vamos a realizar el programa 9.4 con Scilab
s=%s;
g=10*(s+0.1)/((s+0.5)*s*(s+1));
w=0.5:0.01:1.15;
gs=syslin('c',0.13*g);
gs2=syslin('c',0.188*g);
gr=horner(gs,%i*w);
gr2=horner(gs2,%i*w);
theta=atan(imag(gr),real(gr));
theta2=atan(imag(gr2),real(gr2));
ro=abs(gr);
ro2=abs(gr2);
clf;
k=0:0.01:2*%pi;
nr=cos(k)+%i*sin(k);
theta3=atan(sin(k),cos(k));
ro3=abs(nr);
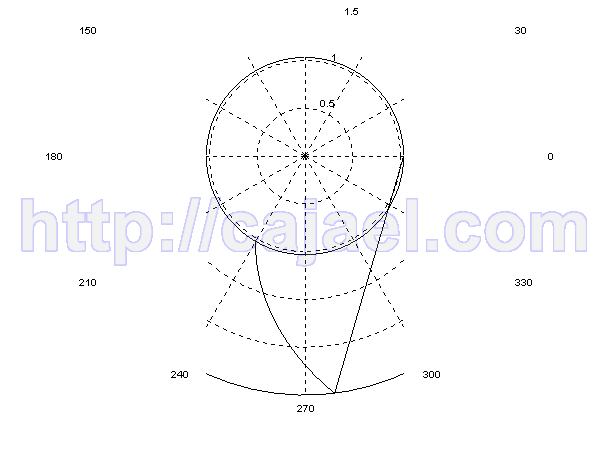
polarplot([theta3 theta2],[ro3 ro2]);
Español



Añadir nuevo comentario