[adsense:responsibe:9545213979]
Problema 1 (Bode, error de posicion, compensador de atraso)
Solapas principales

SOLUCION:
Apartado 1 (Diseñar razonadamente la red de atraso)
-
Primeramente vamos a calcular la K dada por el error de velocidad
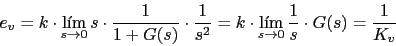
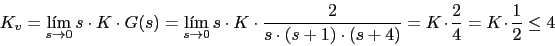
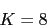 Con lo que el sistema G1(s) nos queda:
Con lo que el sistema G1(s) nos queda: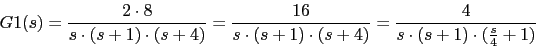
-
Vamos a calcular la nueva frecuencia de cruce wc, sabiendo el margen de fase necesario
w 0.1 0.4 1 4 10 40 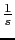
-90 (0) -90 (0) -90 (0) -90 (0) -90 (0) -90 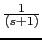
0 (-45) (-45) -45 (-45) (-45) -90 (0) -90 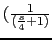
0 (0) 0 (-45) (-45) -45 (-45) (-45) -90 -90 (-45) -117 (-90) -152.81 (-90) (-90) (-45) -270 El valor de wc viene dado por la frecuencia que tiene el siguiente angulo de fase: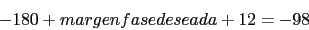
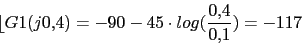
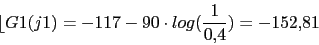
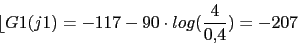
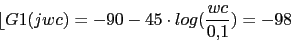
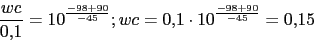 Esta sera la nueva frecuencia de corte
Esta sera la nueva frecuencia de corte -
Vamos a escoger
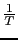 tal que
tal que
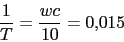
4. Vamos a calcular ![]()
![]()
![]()
| w | 1 | 4 | |||
|
|
(-20) | (-20) | (-20) | ||
|
|
(0) | (-20) | (-20) | ||
|
|
(0) | (0) | (-20) | ||
| (-20) | 12.04 | (-40) | -12.04 | (-60) |
![]()
![]()
![]()
![]()
Con lo que ya tenemos casi el compensador:
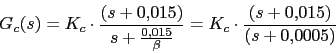
5. Ahora vamos a calcular la ![]()
![]()
![]()
Con lo que el compensador nos queda:
![]()
La fase en wc del sistema es:
![]()
Con lo que el margen de fase como vemos a continuacion verifica las condiciones
Vamos a calcular el margen de ganancia
| w | 5E-5 | 5E-4 | 1.5E-3 | 5E-3 | 1.5E-2 | 1.5E-1 | |||||
|
|
0 | (-45) | -45 | (-45) | (-45) | -90 | (0) | -90 | (0) | -90 | |
|
|
0 | (0) | 0 | (0) | 0 | (45) | (45) | 45 | (45) | 90 | |
| G1(s) | 0 | (-45) | -45 | (-45) | (0) | (45) | -45 | (45) | 0 | ||
| -90 | (0) | -90 | (0) | -90 | (0) | -90 | (0) | -90 | () |
![]()
![]()
![]()
Verifica las condiciones de margen de ganancia
Apartado 2 (Vamos a calcular el error de posicion del sistema controlado)
![]()
Como el sistema es de tipo I. El error de posicion va a ser cero.
![]()
![]()
![]()
Vamos a hacer los calculos y las comprobaciones de resultados con el Scilab
clear;
s=%s;
g=2/(s*(s+1)*(s+4));
gs=syslin('c',g);
aux=horner(s*gs,0)
kv=4;
k=kv/aux
g1=k*gs
fwc=-180+70+12
wc=0.1*10^((fwc+90)/(-45))
aux2=horner(g1,%i*wc)
aux3=atan(imag(aux2),real(aux2));
aux4=360*aux3/(2*%pi)
a=wc/10;
aux5=20*log10(abs(aux2))
g1015=20*log10(4)-20*log10(0.15)
g04=20*log10(4)-40*log10(4)
bet=10^(g1015/20)
b=a/bet
kc=k/bet
gc=kc*(s+a)/(s+b)
gt=g*gc;
gts=syslin('c',gt);
aux6=horner(gts,%i*5)
aux7=20*log10(abs(aux6))
s1=s/(2*%pi)
gb=2/((s1+0.000000001)*(s1+1)*(s1+4));
gcb=kc*(s1+a)/(s1+b);
gtb=gb*gcb;
gbs=syslin('c',gb);
gcbs=syslin('c',gcb)
gtbs=syslin('c',gtb)
[mg,frg]=g_margin(gtbs)
[mp,frp]=p_margin(gtbs)
clf;
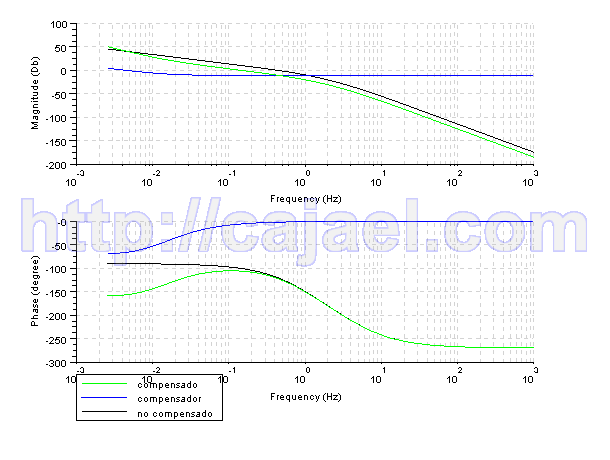
bode([gbs;gcbs;gtbs],['compensado';'compensador';'no compensado'])
Español



Añadir nuevo comentario