[adsense:responsibe:9545213979]
Cuestion 4 (Sistema Discreto, lugar de las raices)
Solapas principales

SOLUCION:
-
Polos y ceros
Cero en 2Polos:
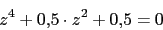
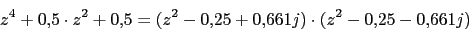
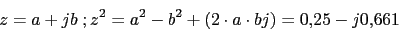
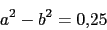
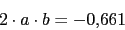
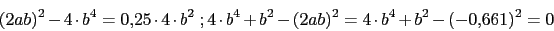
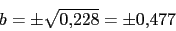
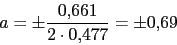
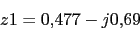
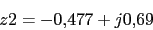
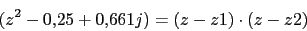
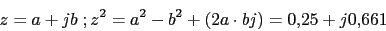
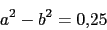
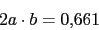
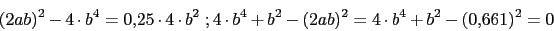
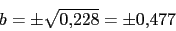
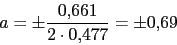
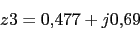
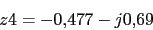
Ya tenemos todos los polos. El numero de ramas en el infinito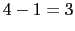
2. El lugar de las raices en el eje real
A la izquierda del cero en 2
-
3. Asintotas
![\begin{displaymath}\theta=\frac{180\cdot(2\cdot k+1)}{3}=[60,-180,-60]\end{displaymath}](http://cajael.com/regulacion/2008ExamsRegulacionII/img243.png)
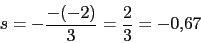
-
4. Puntos de ruptura y ingreso
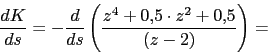
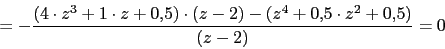
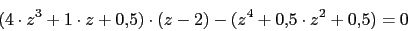
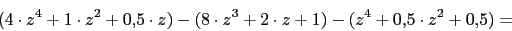
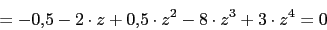
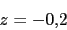
-
5. Angulos de salida
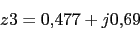
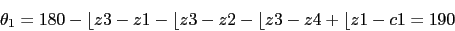
z1 es simetrico con respecto a z3 respecto al eje real.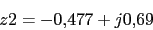
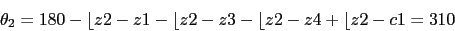
-
z4 es simetrico con respecto a z2 respecto al eje real
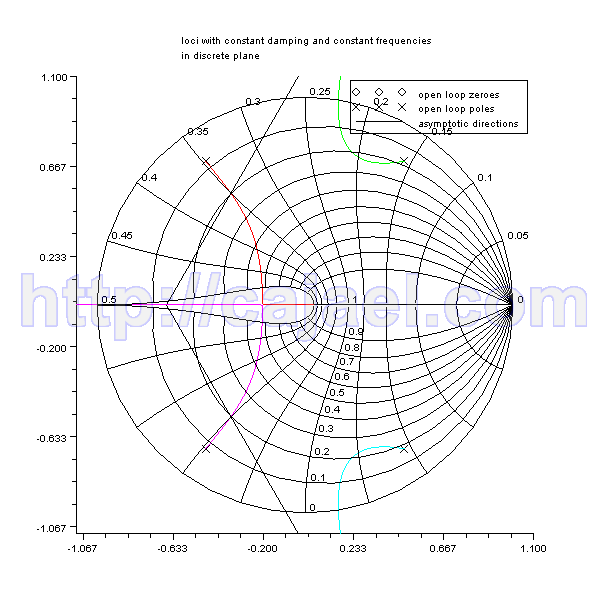
Representacion y calculos hechos con el Scilab
z=%z;
g=(z-2)/(z^4+0.5*z^2+0.5);
gz=syslin('d',g);
clf;
evans(gz,2)
zgrid;
p=roots(denom(g))
tet=%pi-atan(imag(p(1)-p(2)),real(p(1)-p(2)))-atan(imag(p(1)-p(3))
,real(p(1)-p(3)))-atan(imag(p(1)-p(4)),real(p(1)-p(4)))
+atan(imag(p(1)-2),real(p(1)-2))
angz1=360*tet/(2*%pi)
tet2=%pi-atan(imag(p(3)-p(1)),real(p(3)-p(1)))-atan(imag(p(3)-p(2))
,real(p(3)-p(2)))-atan(imag(p(3)-p(4)),real(p(3)-p(4)))
+atan(imag(p(3)-2),real(p(3)-2))
angz1=360*tet2/(2*%pi)
dg=derivat(1/gz)
rdg=roots(numer(dg))
Español



Añadir nuevo comentario