[adsense:responsibe:9545213979]
Cuestion 2 (Regulado derivativo, error de posicion)
Solapas principales

Solucion:
-
Primeramente vamos a calcular el polo dominante
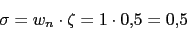
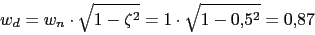
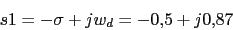
-
Vamos a calcular el angulo del sistema en el polo dominante. Con este angulo calcularemos el angulo necesario para la red de adelanto
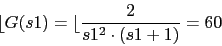
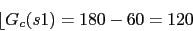
-
Vamos a calcular la red de adelanto
El angulo de un cero en el pto cero con el polo dominante es 120
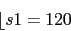 Con lo que un regulador derivativo nos llega
Con lo que un regulador derivativo nos llega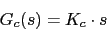
-
Vamos a calcular la
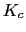 del regulador
del regulador
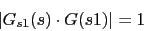
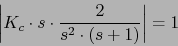
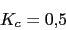 El regulador nos queda:
El regulador nos queda: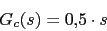
-
Vamos a calcular el error de posicion
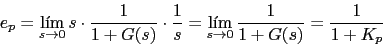
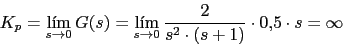
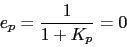
Calculos y comprobaciones con Scilab
//Calculo polo dominante
sig=0.5;
wd=sqrt(1-0.5^2)
s1=-sig+%i*wd
//Calculo del angulo del sistema
s=%s;
g=2/((s+1)*s^2);
gs=syslin('c',g);
aux=horner(gs,s1);
aux1=atan(imag(aux),real(aux));
aux2=360*aux1/(2*%pi)
//Calculo del angulo de la red de adelanto
ac3=180-aux2
//Angulo de un cero en 0 con s1
ac=atan(imag(s1),real(s1));
axc=360*ac/(2*%pi)
//kc del compensador
ax3=horner(s*gs,s1);
abgts1=abs(ax3);
kc=1/abgts1
//Comprobacion de resultados
gc=kc*s;
gt=g*gc;
gts=syslin('c',gt)
gts1=horner(gts,s1)
axgts1=atan(imag(gts1),real(gts1));
agts1=360*axgts1/(2*%pi)
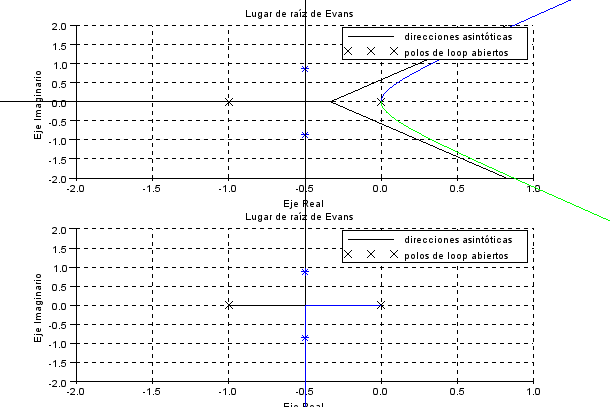
//Lugar de las raices sistema no compensado y compensado
clf;
subplot(2,1,1)
evans(gs)
plot(real(s1),imag(s1),'*');
plot(real(s1),-imag(s1),'*');
xgrid;
mtlb_axis([-2 1 -2 2])
subplot(2,1,2)
evans(gts)
plot(real(s1),imag(s1),'*');
plot(real(s1),-imag(s1),'*');
xgrid;
mtlb_axis([-2 1 -2 2])
Español



Añadir nuevo comentario