[adsense:responsibe:9545213979]
Cuestion 3 (Sistema Discreto, estabilidad, criterio de Jury)
Solapas principales

Solucion:
Vamos a utilizar el criterio de estabilidad de Jury para verificar la estabilidad. La Ecuacion caracteristica sera:
![]()
![]()
El criterio tiene que verificar:
-
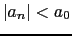
-
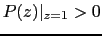
-
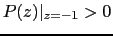 si n par y
si n par y
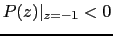 si n impar
si n impar -
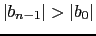
- ....
La primera condicion no se verifica 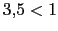 con lo que no es estable
con lo que no es estable
Calculos y comprobacion con scilab
z=%z;
g=2*(z-2)/(z^4+0.5*z^2+0.5)
gz=syslin('d',g)
//Ecuacion caracteristica
ec=numer(gz)+denom(gz)
//Comprobacion mediante transformacion bilineal y Routh
s=%s
z1=(s+1)/(s-1)
g1=2*(z1-2)/(z1^4+0.5*z1^2+0.5)
gs1=syslin('c',g1)
axec2=numer(gs1)+denom(gs1);
ec2=numer(axec2)
routh_t(ec2)
-->routh_t(ec2)
ans =
1.8888889 3.3333333 - 0.3333333
- 0.2222222 4.2222222 0.
39.222222 - 0.3333333 0.
4.2203336 0. 0.
- 0.3333333 0. 0.
Español



Añadir nuevo comentario