Mensaje de error

  • Deprecated function: The each() function is deprecated. This message will be suppressed on further calls en book_prev() (línea 775 de /home1/montes/public_html/drupal/modules/book/book.module).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Deprecated function: implode(): Passing glue string after array is deprecated. Swap the parameters en drupal_get_feeds() (línea 394 de /home1/montes/public_html/drupal/includes/common.inc).

Ejemplo 8-22 pag567 OGATA

Solapas principales

Enviado por pichu en Mié, 06/20/2012 - 19:05

IMPORTANTE el calculo de margenes de fase y ganancia no funcionan bien en la version 5.0.3 de Scilab da el siguiente error:(!-error 27 Division by zero...), en la 4.1.2 si que funcionan. Este problema es debido a s en el denominador para resolverlo hay que hacer una aproximacion s=s+0.000000001 y ya funciona. El programa de este ejemplo lo hice en la 4.

 

Vamos a calcular los margenes de fase y ganancia del sistema con realimentacion unitaria cuando en lazo abierto tiene la siguiente funcion de transferencia:

 

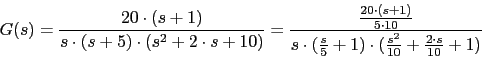
Funcion de transferencia del sistema en lazo abierto. Transformada de Laplace


 

solucion:
Los valores de la ganancia vendrian dados por la siguiente tabla:

 

 
$w=0.1$

$20\cdot log(20)-20\cdot log(50)-20\cdot log(0.1)$

$\frac{20}{50\cdot s}$

$0.1 < w \leq 1$

$-7.95-20\cdot log(w)$

$\frac{20}{50\cdot s}$

$1 < w \leq \sqrt{10}$

$-7.95-20\cdot log(w)+20\cdot log(w)$

$\frac{20\cdot (s+1)}{50\cdot s}$

$\sqrt{10} < w \leq 5$

$-7.95-40\cdot log(\frac{w}{\sqrt{10}})$

$\frac{20\cdot (s+1)}{50\cdot s \cdot (\frac{s^{2}}{10}+\frac{2\cdot s}{10}+1)}$
$w > 5$

$-15.92-60*log(w/5)$

$\frac{20\cdot (s+1)}{50\cdot s \cdot (\frac{s^{2}}{10}+\frac{2\cdot s}{10}+1)\cdot (\frac{s}{5}+1)}$

Los valores de la ganancia en distintos puntos son:

 

 
w Ganancia
0.1 12.04
1 -7.95
$\sqrt(10)$ -7.95
5 -15.95
10 -33.97

Los valores de la fase vendrian dados por:
fase de

angulo de fase de la funcion de transferencia

Los valores de la fase en distintos puntos son:

 

 
w Fase
0.1 -98
1 -68.83
$\sqrt(10)$ -139.85
5 -202.61
10 -236.61

 

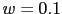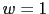La frecuencia de cruce de ganancia sera entre $w=0.1$ y $w=1$ . Con lo que:

 

ganancias igual a 1


 

La frecuencia de cruce sera en 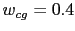$w_{cg}=0.4$. Con lo que calculando la fase para esa frecuencia:
fase de

el valor del angulo de fase en la frecuencia de cruce de ganancia

Con lo que el margen de fase es:

margen de fase

La frecuencia de cruce de fase sera la obtenida mediante esta formula:

 

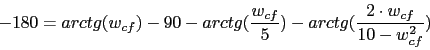
angulo de la funcion de transferencia igual a -180


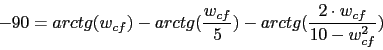
angulo de la funcion de transferencia igual a -180 parte2

 

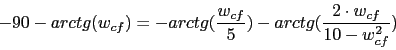
angulo de la funcion de transferencia igual a -180 parte3

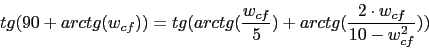
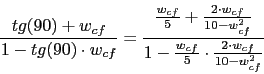
angulo de la funcion de transferencia igual a -180 parte4


angulo de la funcion de transferencia igual a -180 parte4

 

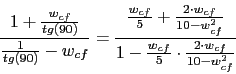
angulo de la funcion de transferencia igual a -180 parte5


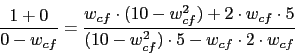
angulo de la funcion de transferencia igual a -180 parte6


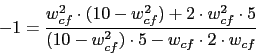
angulo de la funcion de transferencia igual a -180 parte7


angulo de la funcion de transferencia igual a -180 parte8


angulo de la funcion de transferencia igual a -180 parte9

 

angulo de la funcion de transferencia igual a -180 parte10


 


De esta ultima ecuacion obtenemos $w_{cf}=4.01$ sustituyendo esta frecuencia en la siguinte ecuacion:

$-7.95-40\cdot log(\frac{w_{cf}}{\sqrt{10}})=-12.08$

obtenemos un margen de ganancia de 12.08dB

Como los dos margenes el de fase y el de ganancia son positivos el sistema es estable.

 

Ahora lo vamos a calcular con el Scilab:

 

Programa en Scilab

s=%s/(2*%pi);
g=20*(s+1)/(s*(s+5)*(s^2+2*s+10));
gs=syslin('c',g)
[gg,wcp]=g_margin(gs)
[pg,wcg]=p_margin(gs)
margenfase=180+pg

Resultados:
	
wcp  =

    4.0130645
 gg  =

    9.9292942   
   
 wcg  =

    0.4426366
 pg  =

  - 76.342732 
  
margenfase  =

    103.65727
Como se ve los valores cambian un poco pero es debido que la representacion que hicimos anteriormente es una aproximacion

 

Tags:

Español

Añadir nuevo comentario

Más información sobre los formatos de texto

Plain text

  • No se permiten etiquetas HTML.
  • Las direcciones de las páginas web y las de correo se convierten en enlaces automáticamente.
  • Saltos automáticos de líneas y de párrafos.
Pin It