[adsense:responsibe:9545213979]
Resolucion apartado b.1) de la cuestion 3 EDiferenciales 1106S1 (Metodo seleccion, Ecuacion diferencial coeficientes constantes)
Solapas principales
[adsense:336x280:9156825571]
b.1)
Resolucion:
Vamos a obtener la solucion particular de la ecuacion diferencial de coeficientes constantes mediante el metodo de seleccion:
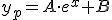
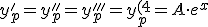
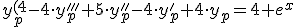
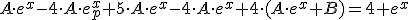
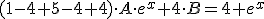
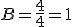
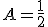
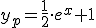
Programa en Sagemath para comprobar la resolucion de la ecuacion diferencial con coeficientes constantes calculada con el metodo de seleccion:
sage:var('x C1 C2 C3 c4')
sage:yp=1+(e^x)/2
sage:y1=(C1+C2*x)*e^(2*x)+(C3*cos(x)+C4*sin(x))
sage:y=yp+y1
sage:f2=diff(y,x,x,x,x)-4*diff(y,x,x,x)+5*diff(y,x,x)-4*diff(y,x)+4*y
sage:f2
Resultado de la ecuacion con Sage
e^x + 4
Español
google+:



Añadir nuevo comentario