[adsense:responsibe:9545213979]
Problema 2 (Diagrama polar, criterio de estabilidad de Nyquist)
Solapas principales

Solucion:
Vamos a calcular el modulo y el angulo en frecuencia.
![]()
![]()
Para calcular la frecuencia a la que el diagrama polar cruza con el eje real. Vamos a utilizar una aproximacion.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
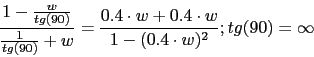
![]()
![]()
![]()
![]()
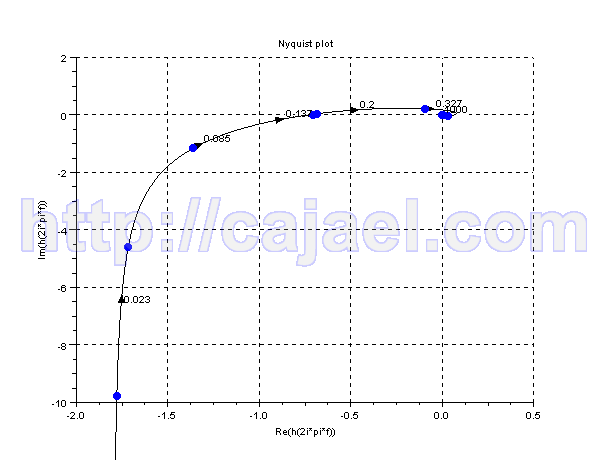
El punto de corte esta mas o menos en 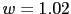
| w | 0.1 | 0.5 | 0.99 | 1.02 | 2 | 5 | 10 |
| fase | -100.29 | -139.48 | -180.09 | -182.32 | -245 | -397.87 | -632.65 |
| modulo | 9.95 | 1.78 | 0.71 | 0.68 | 0.22 | 0.039 | 9.95E-3 |
Despues de calcular los valores vemos que hay varios puntos de corte pero el ultimo que corta en el eje real negativo hacia la izquierda es en 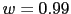 mas o menos. Como la funcion no tiene ningun polo negativo y no da ninguna vuelta alrededor del -1. El sistema es estable mientras que
mas o menos. Como la funcion no tiene ningun polo negativo y no da ninguna vuelta alrededor del -1. El sistema es estable mientras que 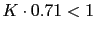 lo que implica que
lo que implica que
![]() .
.
Vamos a comprobarlo con el Scilab:
clf;
w=[0.1 0.2 0.5 1 1.02 2 5 10 20 ]
s=%s;
T=0.8;
pade=(8-4*T*s+(T*s)^2)/(8+4*T*s+(T*s)^2);
g=pade/(s*(s+1));
gs=syslin('c',g);
nyquist(gs);
agr=-(%pi/2)-atan(w)-0.8*w;
agr2=-(%pi/2)-atan(w)-2*atan(w*0.4);
agg=360*agr/(2*%pi);
agg2=360*agr2/(2*%pi);
for i=1:size(agr,2);
m(i)=1/(w(i)*(sqrt(w(i)^2+1)));
v(i)=m(i)*cos(agr(i))+m(i)*sin(agr(i))*%i;
v2(i)=m(i)*cos(agr2(i))+m(i)*sin(agr2(i))*%i;
end;
plot(real(v),imag(v),'.');
mtlb_axis([-2 0.5 -10 0.2]);
xgrid(0.5);
g1=(1+1.4*g);
g2=(1+4*g);
r1=roots(numer(g1))
r2=roots(numer(g2))
Como vemos en los datos siguientes de las raices del denominador en lazo cerrado para 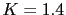 y
y 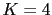 : en
: en 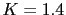 ya hay polos en el semiplano derecho pero practicamente estan en el eje imaginario, en cambio en
ya hay polos en el semiplano derecho pero practicamente estan en el eje imaginario, en cambio en 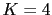 ya hay claramente polos en el semiplano derecho.
ya hay claramente polos en el semiplano derecho.
r1 = 0.0093576 + 0.9848008i 0.0093576 - 0.9848008i - 3.0093576 + 2.9977472i - 3.0093576 - 2.9977472i r2 = 0.4172850 + 1.344734i 0.4172850 - 1.344734i - 3.417285 + 3.6801704i - 3.417285 - 3.6801704i
Español



Añadir nuevo comentario