[adsense:responsibe:9545213979]
Problema 4 (Lugar de las raices)
Solapas principales
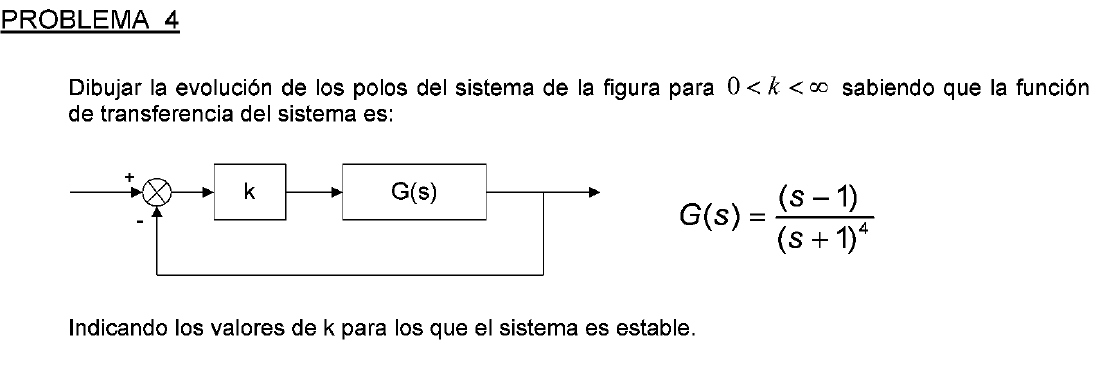
Solucion:
-
Polos,ceros y ramas
ramas=4-1=3
polos: s=-1 (polo multiple)
ceros: s=1 -
Determinacion del lugar de las raices en el eje real(numero impar de polos y ceros a la derecha)
El lugar de las raices esta entre 1 y -1 y a la izquierda del -1.
-
Asintotas
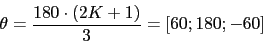
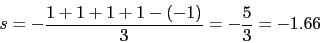
-
Puntos de ingreso y ruptura
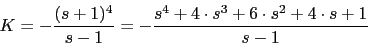
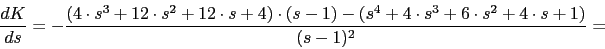
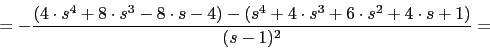
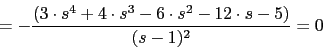 La ecuacion es complicada pero el punto de ruptura va estar en -1 ya que tiene que estar entre dos polos y en la parte del eje real del lugar de las raices.
La ecuacion es complicada pero el punto de ruptura va estar en -1 ya que tiene que estar entre dos polos y en la parte del eje real del lugar de las raices.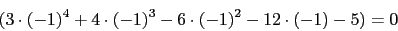
-
Corte con el eje imaginario
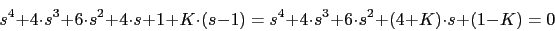 Vamos a utilizar el criterio de Routh
Vamos a utilizar el criterio de Routh1 6 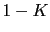
4 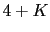
0 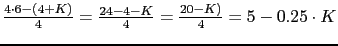
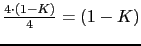
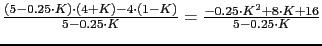
0 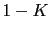 Para que la primera fila sea positiva se tiene que cumplir:
Para que la primera fila sea positiva se tiene que cumplir: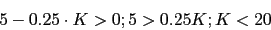
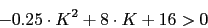 La raices de la ecuacion son
La raices de la ecuacion son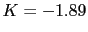 y
y 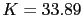 . Con lo que para que se verifique la condicion anterior ya que K es positiva,
. Con lo que para que se verifique la condicion anterior ya que K es positiva, 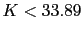 .
.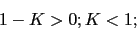 Es decir el sistema es estable para
Es decir el sistema es estable para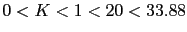 .El sistema corta el eje en
.El sistema corta el eje en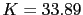
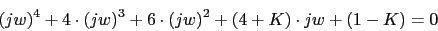
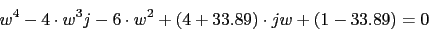
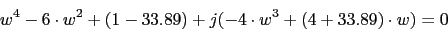
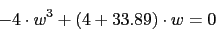
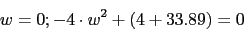
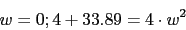
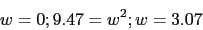 El sistema corta el eje en
El sistema corta el eje en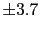
Vamos a calcular el problema con el Scilab
clf;
s=%s;
den=(s+1)^4;
num=(s-1);
g=num/den;
gs=syslin('c',g);
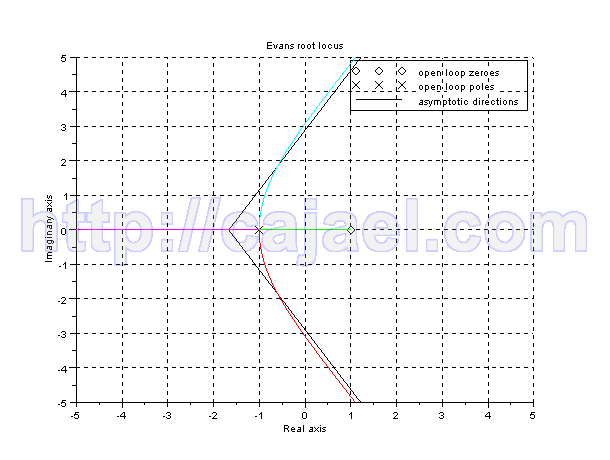
evans(g);
mtlb_axis([-5 5 -5 5]);
xgrid;
gc1=1+1*g;
gc2=1+2*g;
r1=roots(numer(gc1))
r2=roots(numer(gc2))
Resultados: como se ve el 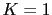 limita la estabilidad (con ganancia dos ya es inestable) y el diagrama de Evans coincide.
limita la estabilidad (con ganancia dos ya es inestable) y el diagrama de Evans coincide.
r1 = 0 - 0.8233950 + 1.2028208i - 0.8233950 - 1.2028208i - 2.35321 r2 = 0.1439011 - 0.7504831 + 1.4374043i - 0.7504831 - 1.4374043i - 2.6429349
Español



Comentarios
Anónimo (no verificado)
Vie, 02/07/2014 - 01:59
Enlace permanente
es un problema bien resuelto
es un problema bien resuelto
Páginas
Añadir nuevo comentario