Mensaje de error

  • Deprecated function: The each() function is deprecated. This message will be suppressed on further calls en menu_set_active_trail() (línea 2394 de /home1/montes/public_html/drupal/includes/menu.inc).
  • Deprecated function: The each() function is deprecated. This message will be suppressed on further calls en book_prev() (línea 775 de /home1/montes/public_html/drupal/modules/book/book.module).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Deprecated function: implode(): Passing glue string after array is deprecated. Swap the parameters en drupal_get_feeds() (línea 394 de /home1/montes/public_html/drupal/includes/common.inc).

Cuestion 1 EDiferenciales 1109S2: Page 4 of 6

Solapas principales

Enviado por Anónimo (no verificado) en Vie, 04/04/2014 - 13:23
[adsense:336x280:9156825571]

Programa en Sagemath para comprobar que la ecuacion diferencial de Riccati nos queda como una ecuacion lineal de primer orden:

sage: function('y')
sage: function('z')
sage: function('yp')
sage: y1(x) =yp(x)+1/z(x)
sage: dg = (1+x^3)*y(x).diff(x)+2*x*y(x)^2+x^2*y(x)+1
sage: f1(x)=dg.substitute_function(y,y1)
sage: f2(x)=expand(f1(x)*z(x)^2-z(x)^2*((1+x^3)*yp(x).diff(x)+2*x*yp(x)^2+x^2*yp(x)+1))
sage: yp(x,A)=A*x
sage: f2(x,A)
Resultado de Sagemath
-x^3*D[0](z)(x) + x^2*z(x) + 4*x*yp(x)*z(x) + 2*x - D[0](z)(x)

c)

Resolucion:

Vamos a resolver la ecuacion diferencial lineal:
z'-\frac{(4\cdot x\cdot A\cdot x+x^2)}{(1+x^3)}\cdot z-\frac{2\cdot x}{(1+x^3)}=0
 
u=e^{\int \frac{(4\cdot x\cdot A\cdot x+x^2)}{(1+x^3)}\,dx }
 
\int \frac{(4\cdot x\cdot A\cdot x+x^2)}{(1+x^3)}\,dx=(4\cdot  A+1)\cdot\int \frac{ x^2}{(1+x^3)}\,dx  
 
 
 
 

Tags:

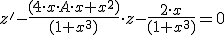
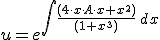
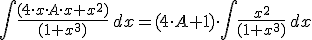
Español

Páginas

Añadir nuevo comentario

Más información sobre los formatos de texto

Plain text

  • No se permiten etiquetas HTML.
  • Las direcciones de las páginas web y las de correo se convierten en enlaces automáticamente.
  • Saltos automáticos de líneas y de párrafos.
Pin It