[adsense:responsibe:9545213979]
Cuestion 3 (Sistemas Discretos, regulador)
Solapas principales

El retenedor siendo
![]()
![]()
El sistema nos quedaria:
![]()
Vamos a descomponer la parte en s de la funcion de transferencia
![]()
![]()
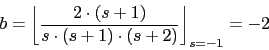
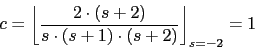
![]()
Ahora hacemos la transformada Z de estas funciones:
![]()
Con lo que nos queda la funcion 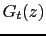
![]()
![]()
Ahora vamos a calcular el polo dominante:
![]()
![]()
![]()
![]()
![]()
El angulo que tiene que tener el regulador:
![]()
![]()
Vamos a necesitar un regulador de atraso
Vamos a situar el polo del regulador en 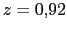 . Con lo que ahora tendremos que calcular el cero.
. Con lo que ahora tendremos que calcular el cero.
![]()
![]()
![]()
![]()
![]()
Vamos a calcular la 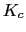 del compensador.
del compensador.
![]()
![]()
![]()
Calculos y comprobaciones con el Scilab
//Descomposicion en fracciones simples
s=%s;
g=2/(s*(s+1)*(s+2));
T=0.1;
gs=syslin('c',g)
gf=tf2ss(gs);
se=pfss(gf)
//Calculo de la transformada Z
a=numer(se(1))
b=numer(se(2))
c=numer(se(3))
z=%z;
gr=(z-1)/z;
aux=(z/(z-1))-(2*z/(z-exp(-T)))+(z/(z-exp(-2*T)))
auxs=syslin('d',aux);
gz=gr*aux
gzs=syslin('d',gz);
r=roots(denom(auxs))
//Vamos a comprobar la funcion de transferencia resultante
gz1=ss2tf(dscr(tf2ss(gs*s),T))
//Polo dominante
sig=4/5;
wd=-(4*%pi)/(5*log(0.1))
z1=exp(-sig*T)*(cos(wd*T)+%i*sin(wd*T))
//Angulo de Gt en z1
aux2=horner(gzs,z1);
aux3=atan(imag(aux2),real(aux2));
aux4=360*aux3/(2*%pi)
//Angulo que debe tener el regulador
aux5=-180-aux4
//Vamos a calcular el cero del regulador;
aux6=-(2*%pi*aux5)/360;
aux7=imag(z1)*tan(aux6)
aux8=real(z1)-aux7
//Parte del regulador
gc=(z-aux8)/(z-real(z1))
gcs=syslin('d',gc)
aux11=horner(gcs,z1)
aux12=atan(imag(aux11),real(aux11));
aux13=360*aux12/(2*%pi)
//vamos a calcular al Kc del regulador
gt=gc*gz;
gts=syslin('d',gt)
aux9=horner(gts,z1);
aux10=abs(aux9)
kc=1/abs(aux10)
//vamos a comprobar los resultados
gt1=kc*gt;
gt1s=syslin('d',gt1)
aux14=horner(gt1s,z1)
aux15=atan(imag(aux14),real(aux14));
aux16=360*aux15/(2*%pi)
aux17=abs(aux14)
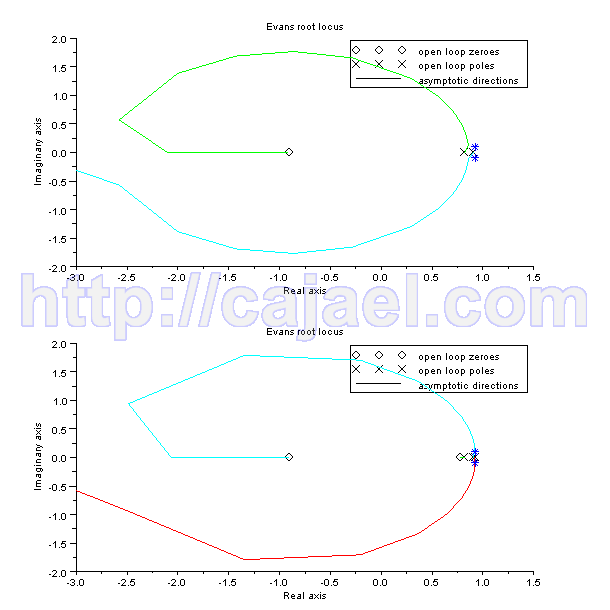
clf;
subplot(2,1,1)
evans(gzs)
plot(real(z1),imag(z1),'*');
plot(real(z1),-imag(z1),'*');
mtlb_axis([-3 1.5 -2 2])
subplot(2,1,2)
evans(gt1s)
plot(real(z1),imag(z1),'*');
plot(real(z1),-imag(z1),'*');
mtlb_axis([-3 1.5 -2 2])
Español



Añadir nuevo comentario