[adsense:responsibe:9545213979]
Mensaje de error
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Deprecated function: The each() function is deprecated. This message will be suppressed on further calls en book_prev() (línea 775 de /home1/montes/public_html/drupal/modules/book/book.module).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Deprecated function: implode(): Passing glue string after array is deprecated. Swap the parameters en drupal_get_feeds() (línea 394 de /home1/montes/public_html/drupal/includes/common.inc).
Se encuentra usted aquí
Cuestion 4 (Sistemas Discretos, sobreoscilacion, intervalo de pico y valor final)
Solapas principales
Enviado por pichu en Vie, 07/06/2012 - 13:02

Solucion:
Vamos a calcular la salida del sistema:
![]()
Vamos a descomponer en fracciones simples:
![]()
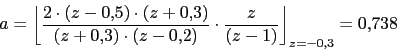
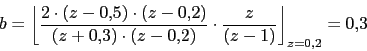
![]()
![]()
Vamos a calcular la transfomada inversa z de esta ecuacion.
![]()
El valor final sera:
![]()
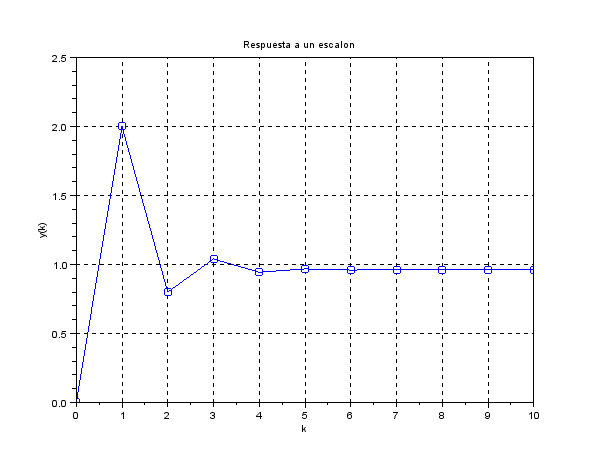
Vamos a calcular los valores de y en funcion de k.
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| y(k) | 0 | 2 | 0.8 | 1.04 | 0.944 | 0.968 | 0.96 | 0.962 | 0.961 |
El intervalo de pico es 1.
El valor de sobreoscilacion es:
![]()
Calculos y comprobacion de resultados mediante el Scilab
clear;
z=%z;
g=2*(z-0.5)/((z+0.3)*(z-0.2));
r=z/(z-1);
gt=g*r
gs=syslin('d',g);
gts=syslin('d',gt);
a=horner((z+0.3)*gts,-0.3)
b=horner((z-0.2)*gts,0.2)
c=horner((z-1)*gts,1)
gt2=a/(z+0.3)+b/(z-0.2)+c/(z-1)
for i=1:1:40
y(i)=a*0.3^(i-1)*cos((i-1)*%pi)+b*0.2^(i-1)+c*1^(i-1);
end;
aux=[0 y'];
k=0:1:40;
x=ones(1,41);
y2=flts(x,gs);
[aux;y2]
aux2=horner(gs,1)
aux3=(max(y)-aux2)/aux2
clf;
plot(k,y2,'o');
plot(k,aux);
mtlb_axis([0 10 0 2.1]);
xgrid;
xtitle('Respuesta a un escalon','k','y(k)')
Tags:
Español

Búsqueda personalizada
Idiomas
 English
English Español
Español
Comentarios recientes
- Muy bueno hace 10 años 3 meses
- good hace 10 años 3 meses
- Engranajes hace 10 años 3 meses
- REVISAR hace 10 años 4 meses
- UTIL hace 10 años 4 meses
- Realimentación hace 10 años 7 meses
- Hello There. I found your hace 10 años 7 meses
- Good web site! I really love hace 10 años 7 meses
- Well I really enjoyed reading hace 10 años 7 meses
- Thanks again for the blog hace 10 años 7 meses
Seguidores en Google
Busquedas populares
Inicio de sesión
Contenido popular
- 6 Problema 1 (Diodos, resistencia dinamica, Shockley)
- Ejercicion 4 (Estabilidad, Criterio de Routh)
- Examenes 2009 RI
- 3.1.2 Calculo de los parámetros híbridos con Micro-Cap
- Problema 1 (Bode, compensador de adelanto, error de velocidad, margen de fase y margen de ganancia)
- SISTEMAS MECANICOS
- Apartada c) del Ejercicio 2 Campos y Ondas 1402S2 (Potencia onda incidente; Potencia onda reflejada; Potencia onda transmitida)
- 1.4.2 Montaje practico del circuito RC en serie
- 1.3 Simulación de un circuito RC en serie
- 2.1.1 Calculo teórico del rectificador de onda completa
- Catalogo de baterias industriales de EXIDE (Ingles)
- 2.1 Calculo teórico y simulación del circuito RC con potenciometro
- Ejemplo 9.2 pag633 OGATA
- 2.4 Medir la intensidad con el osciloscopio en el circuito RC con potenciometro
- Cuestion 2 EDiferenciales 1406S2 (Ecuacion diferencial lineal de coeficientes constantes)
- REGULACION AUTOMATICA
- Problema 1 (Bode, regulador, error de posicion)
- Tranformada de Laplace
- Cuestion 1 EDiferenciales 1109S2
- Cuestion 2 EDiferenciales 1206S1
- SIMULACIONES CON SCILAB
- 1.1.2 Simulación con Micro-Cap del rectificador de media onda
- Apartada 1) del Ejercicio 2 Campos y Ondas 1402S1 (Constantes linea de transmision; Constante de propagacion)
- Simulacion estadistica del Ejercicio 6.8 (Distribucion de Poisson)
- Problema B2.1 pag51 OGATA 4ed(Tranformada de Laplace)
Páginas
Today's popular content
- REGULACION AUTOMATICA
- SIMULACIONES CON SCILAB
- Tranformada de Laplace
- Ejemplo 2.6 pag37 OGATA 4edicion(Tranformada de Laplace)
- Ejemplo 2.7a pag38 OGATA 4edicion(Tranformada de Laplace)
- Ejemplo 2.7b pag39 OGATA 4edicion(Tranformada de Laplace)
- Ejemplo 2.10 pag46 OGATA 4ed(Tranformada de Laplace)
- Problema A2.15 pag48 OGATA 4ed(Tranformada de Laplace)
- Problema A2.16 pag49 OGATA 4ed(Tranformada de Laplace)
- Ejemplo 2.17 pag50 OGATA 4ed(Tranformada de Laplace)
- Problema B2.1 pag51 OGATA 4ed(Tranformada de Laplace)
- Problema B2.2 pag51 OGATA 4ed(Tranformada de Laplace)
- Problema B2.3 pag51 OGATA 4ed(Tranformada de Laplace)
- Lugar de las Raices
- Programa 6.1 OGATA 4edicion pag360 (Lugar de las Raices)
- Programa 6.2 OGATA 4edicion pag361 (Lugar de las Raices)
- Programa 6.3 OGATA 4edicion pag362 (Lugar de las Raices)
- Programa 6.5 OGATA 4edicion pag366 (Lugar de las Raices)
- Programa 6.6 OGATA 4edicion pag367
- Programa 6.7 OGATA 4edicion pag367
- Programa 6.8 OGATA 4edicion pag370
- Programa 6.9 OGATA 4edicion pag372
- Programa 6.10 OGATA 4edicion pag378
- Problema A6.11 OGATA 4edicion pag400
- Problema A6.12 OGATA 4edicion pag402


Añadir nuevo comentario