[adsense:responsibe:9545213979]
Cuestion 2 (Respuesta en frecuencia, compensador de adelanto)
Solapas principales

SOLUCION:
-
Vamos a calcular el error de velocidad del sistema
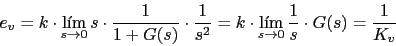
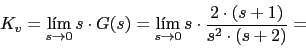
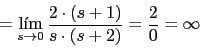
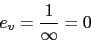
-
Vamos calcular el margen de fase del sistema y con el margen de fase del compensador
w 1 2 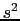
-40 -40 -40 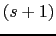
0 20 20 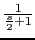
0 0 -20 -40 -20 -40 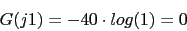
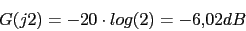
La frecuencia de corte sera en 1. Con lo que podremos calcular el margen de fase del sistema.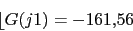
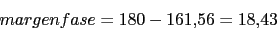 Vamos a calcular la fase que proporcionara el compensador de adelanto para que el margen de fase sea 30
Vamos a calcular la fase que proporcionara el compensador de adelanto para que el margen de fase sea 30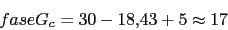
-
Vamos a calcular los parametros del compensador de adelanto
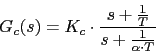
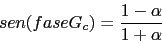
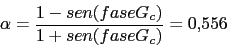 Ahora vamos a calcular la nueva frecuencia de corte wc
Ahora vamos a calcular la nueva frecuencia de corte wc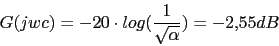
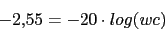
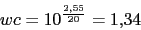
![]()
![]()
![]()
Como la constante de error de velocidad es infinito le vamos a dar a 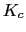 el valor 1.8
el valor 1.8
![]()
-
4. Vamos a comprobar el margen de fase del sistema resultante
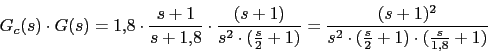
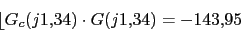
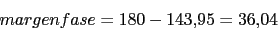 Cumple las condiciones de margen de fase
Cumple las condiciones de margen de fasew 0.1 0.18 0.2 1 1.8 2 10 18 20 
-174 -170 -169 -145 -145 -146 -169 -174 -174 Las condiciones de margen de ganancia tambien las cumple nunca se cruza el sistema con -180
Calculos,comprobaciones y diagrama de Bode utilizando el Scilab
s=%s;
g=2*(s+1)/(s^2*(s+2));
gs=syslin('c',g);
gs1=horner(gs,%i);
angg1=(360/(2*%pi))*atan(imag(gs1),real(gs1));
mfg=180+angg1
anggc=30-mfg+5
aux=sin((2*%pi/360)*anggc);
alp=(1-aux)/(1+aux)
g1wc=-20*log10(1/sqrt(alp))
wc=10^(g1wc/(-20))
a=sqrt(alp)*wc
b=a/alp
gc=(s+a)/(s+b)
gc1=(s+1)/(s+1.8)
gt=gc1*g;
gts=syslin('c',gt);
g134=horner(gts,%i*1.34);
anggt=(360/(2*%pi))*atan(imag(g134),real(g134))
mfgt=180+anggt
g134=20*log10(1/1.8);
w=[0.1 0.18 0.2 1 1.8 2 10 18 20];
gw=horner(gts,%i*w);
anggtw=(360/(2*%pi))*atan(imag(gw),real(gw))
s1=s/(2*%pi)
gb=2*(s1+1)/((s1+000000.1)^2*(s1+2));
gbc1=1.8*(s1+1)/(s1+1.8);
gbt=gb*gbc1;
gbs=syslin('c',gb);
gbcs=syslin('c',gbc1);
gbts=syslin('c',gbt);
//margen real de fase y de ganancia
[mf,frp]=p_margin(gbts)
[mg,frg]=g_margin(gbts)
clf;
bode([gbs;gbcs;gbts],0.1,100,['compensado';'compensador';'no compensado'])
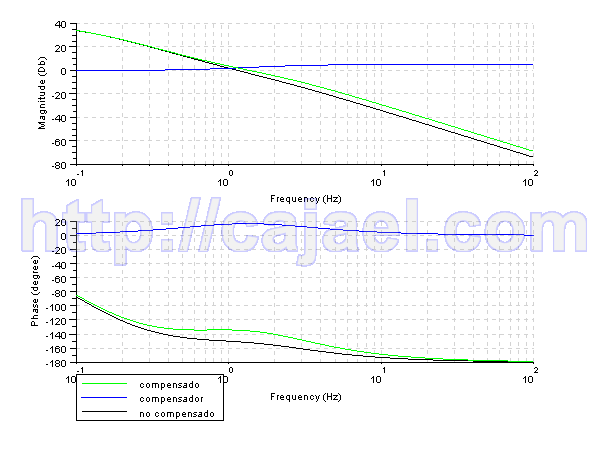
Español



Añadir nuevo comentario