[adsense:responsibe:9545213979]
1.4 Simulacion estadistica de la varianza del Ejercicio 1.1
Solapas principales
[adsense:336x280:9156825571]
En los programas de simulacion utilizan la siguiente varianza:
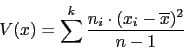
Cuando en el ejercicio se utiliza esta varianza:
![]()
La solucion es multiplicar la varianza de la simulacion por:
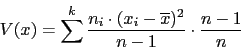
-
Simulacion estadistica de la varianza con R-Project
> x <- c(rep(47,1),rep(48,3),rep(49,2),rep(50,8),rep(51,3),rep(52,2) ,rep(53,1)); > ni<- table(x); > n<-sum(ni) > var(x)*(n-1)/n [1] 2.1475
-
Simulacion estadistica de la varianza con Mathematica
x := Join[ConstantArray[47, 1], ConstantArray[48, 3], ConstantArray[49, 2], ConstantArray[50, 8], ConstantArray[51, 3], ConstantArray[52, 2], ConstantArray[53, 1]]; ni := Tally [x]; n := Sum[ni[[i, 2]], {i, Length[ni]}]; (Variance[x] (n - 1))/n; N[%] 2.1475`
Español



Comentarios recientes