Mensaje de error

  • Deprecated function: The each() function is deprecated. This message will be suppressed on further calls en menu_set_active_trail() (línea 2394 de /home1/montes/public_html/drupal/includes/menu.inc).
  • Deprecated function: The each() function is deprecated. This message will be suppressed on further calls en book_prev() (línea 775 de /home1/montes/public_html/drupal/modules/book/book.module).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Deprecated function: implode(): Passing glue string after array is deprecated. Swap the parameters en drupal_get_feeds() (línea 394 de /home1/montes/public_html/drupal/includes/common.inc).

Apartada a) de la cuestion 2 EDiferenciales 1206S2 (Ecuacion diferencial lineal; Punto ordinario): Page 2 of 2

Solapas principales

Enviado por Anónimo (no verificado) en Jue, 05/29/2014 - 13:49
[adsense:336x280:9156825571]
a_{n+2}=-\frac{(n+1)}{(n+2)\cdot (n+1)}\cdot a_{n}
 
a_{n}=-\frac{(n+1-2)}{(n+2-2)\cdot (n+1-2)}\cdot a_{n-2}
 
a_{n}=-\frac{(n-1)}{n\cdot (n-1)}\cdot a_{n-2}=-\frac{1}{n}\cdot a_{n-2}
 
a_{2}=-\frac{1}{2}\cdot a_{0}
a_{3}=-\frac{1}{3}\cdot a_{1}
a_{4}=-\frac{1}{4}\cdot a_{2}=-\frac{1}{4}\cdot -\frac{1}{2}\cdot a_{0}=\frac{1}{8}\cdot a_{0}
a_{5}=-\frac{1}{5}\cdot a_{3}=-\frac{1}{5}\cdot -\frac{1}{3}\cdot a_{1}=\frac{1}{15}\cdot a_{1}
 
 
y=a_0\cdot \left(1-\frac{x^2}{2}+\frac{x^4}{8}\right)+a_1\cdot \left(x-\frac{x^3}{3}+\frac{x^5}{15}\right)
 
 
 
 
 
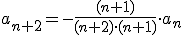
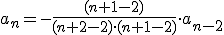
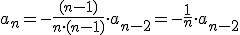
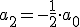
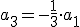
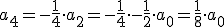
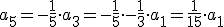
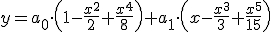
Programa en Sagemath para comprobar los desarrollos en serie de potencias de la ecuacion diferencial
sage: var('x a0 a1')
sage: g=[a0,a1]
sage: y=g[0]+g[1]*x
n=5
sage: for i in range(2,n):
sage:     a=-(1/i)*g[i-2]
sage:     g.append(a)
sage: for i in range(2,n):
sage:     y=g[i]*x^i+y
sage: r=diff(y,x,x)+x*diff(y,x)+y
sage: r.expand(),y

Resultado de la ecuacion diferencial:
(2/5*a1*x^5 + 5/8*a0*x^4, 1/15*a1*x^5 + 1/8*a0*x^4 - 1/3*a1*x^3 -
1/2*a0*x^2 + a1*x + a0)

Que se puede considerar practicamente cero cuanto mas elevemos el valor de n tendiendolo hacia el infinito
 

Tags:

Español
google+: 
View profile on Google+

Páginas

Añadir nuevo comentario

Más información sobre los formatos de texto

Plain text

  • No se permiten etiquetas HTML.
  • Las direcciones de las páginas web y las de correo se convierten en enlaces automáticamente.
  • Saltos automáticos de líneas y de párrafos.
Pin It