Mensaje de error

  • Deprecated function: The each() function is deprecated. This message will be suppressed on further calls en book_prev() (línea 775 de /home1/montes/public_html/drupal/modules/book/book.module).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Deprecated function: implode(): Passing glue string after array is deprecated. Swap the parameters en drupal_get_feeds() (línea 394 de /home1/montes/public_html/drupal/includes/common.inc).

Cuestion 2 (regulador PI, error de posicion)

Solapas principales

Enviado por pichu en Vie, 07/13/2012 - 13:21

Image 2008Sept1C2

SOLUCION:
Primero vamos a calcular el polo dominante que queremos:

\begin{displaymath}\sigma=w_{n}\cdot \zeta =1\cdot 0.5=0.5\end{displaymath}


 

\begin{displaymath}w_{d}=w_{n}\cdot \sqrt{1-\zeta^{2}}=\frac{\sqrt{3}}{2}=0.866\end{displaymath}


 

\begin{displaymath}s1=-0.5+j\cdot 0.866\end{displaymath}


 

Ahora vamos a obtener el angulo de fase que tenemos para este polo del sistema

\begin{displaymath}\lfloor{G(s1)}=\lfloor{\frac{2}{(s1+1)^{2}}}=-120\end{displaymath}


 

Como se ve necesitamos hacer un atraso de 60 grados para situarnos en -180. El regulador que utilizaremos sera un PI

\begin{displaymath}G_{c}(s)=K_{c}\cdot \frac{(s+a)}{s}\end{displaymath}


 

\begin{displaymath}\lfloor{G_{c}(s1)}=-(-180-tg^{-1}(\frac{0.866}{0.5}))+tg^{-1}(\frac{0.866}{a-0.5})=-60\end{displaymath}


 

\begin{displaymath}tg^{-1}(\frac{0.866}{a-0.5})=60\end{displaymath}


 

\begin{displaymath}\frac{0.866}{a-0.5}=tg(60);\frac{0.866}{tg(60)}=a-0.5;a=0.5+\frac{0.866}{tg(60)}=1\end{displaymath}


 

Con lo que el regulador nos quedara:

\begin{displaymath}G_{c}(s)=K_{c}\cdot \frac{(s+1)}{s}\end{displaymath}


 

Ahora calcularemos la 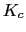$K_{c}$

\begin{displaymath}\left\vert K_{c}\cdot \frac{(s1+1)}{s1} \cdot \frac{2}{(s1+1)^{2}}\right\vert=1\end{displaymath}


 

\begin{displaymath}K_{c}\cdot 2=1\; ;K_{c}=0.5\end{displaymath}


 

\begin{displaymath}G_{c}(s)=0.5\cdot \frac{(s+1)}{s}\end{displaymath}


 

El sistema sera:

\begin{displaymath}G(s)\cdot G_{c}(s)=K_{c}\cdot \frac{(s+1)}{s}\cdot \frac{2}{(s+1)^{2}}\end{displaymath}


 

El error de posicion es cero por ser de tipo 1 el sistema compensado.

 

Vamos a hacer los calculos y las comprobaciones de resultados con el Scilab

 

s=%s;
zet=0.5;
wn=1;
sig=zet*wn
wd=wn*sqrt(1-zet^2)
s1=-sig+%i*wd
g=2/((s+1)^2);
gs=syslin('c',g);
aux=horner(gs,s1);
aux2=atan(imag(aux),real(aux));
anggs1=360*aux2/(2*%pi)
anggc=-180-anggs1
aux3=atan(imag(s1),real(s1));
angs1=360*aux3/(2*%pi)
aux4=anggc+angs1
aux5=(2*%pi)*aux4/360;
a=sig+(wd/tan(aux5))
aux6=(s+a)/s;
aux7=aux6*gs;
aux8=abs(horner(aux7,s1))
kc=1/aux8
gc=kc*aux6;
gt=g*gc;
gts=syslin('c',gt)
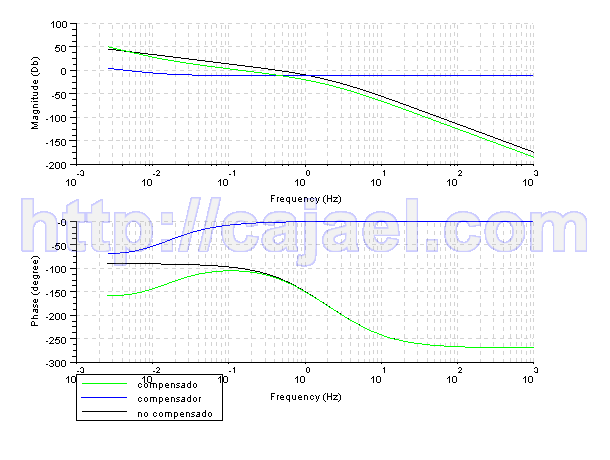
clf;
evans(gts)
plot(real(s1),imag(s1),'*')
plot(real(s1),-imag(s1),'*')
mtlb_axis([-2 1 -1.5 1.5])
Image P2sept2008ps

 

Tags:

Español

Añadir nuevo comentario

Más información sobre los formatos de texto

Plain text

  • No se permiten etiquetas HTML.
  • Las direcciones de las páginas web y las de correo se convierten en enlaces automáticamente.
  • Saltos automáticos de líneas y de párrafos.
Pin It