Mensaje de error

  • Deprecated function: The each() function is deprecated. This message will be suppressed on further calls en book_prev() (línea 775 de /home1/montes/public_html/drupal/modules/book/book.module).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Deprecated function: implode(): Passing glue string after array is deprecated. Swap the parameters en drupal_get_feeds() (línea 394 de /home1/montes/public_html/drupal/includes/common.inc).

Cuestion 2 (Bode,compensador proporcional)

Solapas principales

Enviado por pichu en Mié, 07/11/2012 - 13:21
Image 2008Jun2C2
SOLUCION:
  • Primeramente vamos a calcular la K dada por el error de velocidad

     




     

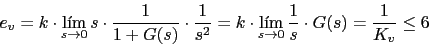
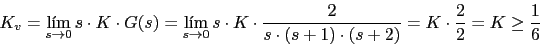
  • Vamos a calcular el diagrama de Bode para la funcion

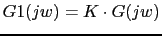
    $G1(jw)=K\cdot G(jw)$

     


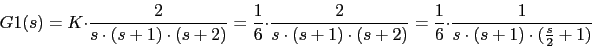
    Las ganancias: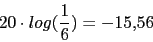

    \begin{displaymath}20\cdot log(\frac{1}{6})=-15.56\end{displaymath}


     

    w   1   2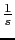  
    $\frac{1}{s}$ (-20) 0 (-20)   (-20)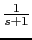

    $\frac{1}{ s+1}$

    		 (0) 0 (-20) 0 (-20)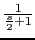

    $\frac{1}{\frac{s}{2}+1}$

    		 (0) 0 (0) 0 (-40)
      (-20) -15.56 (-40)   (-60)

    Vamos a calcular las fases
    w 0.1   0.2   1   2   10   20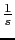
    $\frac{1}{s}$ -90 (0) -90 (0) -90 (0) -90 (0) -90 (0) -90

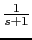
    $\frac{1}{ s+1}$

    		 0 (-45)   (-45) -45 (-45)   (-45) -90 (0) -90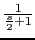

    $\frac{1}{\frac{s}{2}+1}$

    		 0 (0) 0 (-45)   (-45) -45 (-45)   (-45) -90
      -90 (-45) -103 (-90) -166 (-90) -193 (-90)   (-45) -270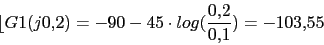

     

    \begin{displaymath}\lfloor{G1(j0.2)=-90-45\cdot log(\frac{0.2}{0.1})}=-103.55\end{displaymath}

     

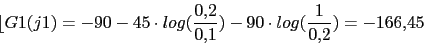
    \begin{displaymath}\lfloor{G1(j1)}=-90-45\cdot log(\frac{0.2}{0.1})-90\cdot log(\frac{1}{0.2})=-166.45\end{displaymath}

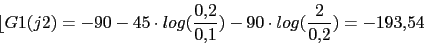
    \begin{displaymath}\lfloor{G1(j2)}=-90-45\cdot log(\frac{0.2}{0.1})-90\cdot log(\frac{2}{0.2})=-193.54\end{displaymath}


     

  • Vamos a calcular el margen de fase. Primero calcularemos la frecuencia de cruce de ganancia

     

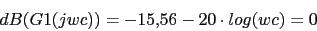
    \begin{displaymath}dB(G1(jwc))=-15.56-20\cdot log(wc)=0\end{displaymath}

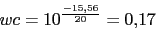
    \begin{displaymath}wc=10^{\frac{-15.56}{20}}=0.17\end{displaymath}


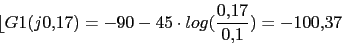
    \begin{displaymath}\lfloor{G1(j0.17)}=-90-45\cdot log(\frac{0.17}{0.1})=-100.37\end{displaymath}

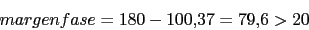
    \begin{displaymath}margenfase=180-100.37=79.6>20\end{displaymath}


     

  • Vamos a calcular el margen de ganancia. Primero calcularemos la frecuencia de cruce de fase

     

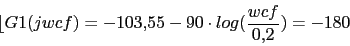
    \begin{displaymath}\lfloor{G1(jwcf)}=-103.55-90\cdot log(\frac{wcf}{0.2})=-180\end{displaymath}


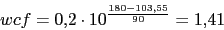
    \begin{displaymath}wcf=0.2\cdot 10^{\frac{180-103.55}{90}}=1.41\end{displaymath}

     

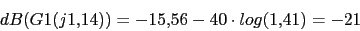
    \begin{displaymath}dB(G1(j1.14))=-15.56-40\cdot log(1.41)=-21\end{displaymath}


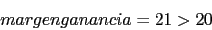    \begin{displaymath}margenganancia=21>20\end{displaymath}


     

    Con lo que si multiplicamos el sistema por una 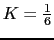$K=\frac{1}{6}$ el sistema cumple las condiciones. Lo que necesitamos es un regulador proporcional.

     

Comprobaciones y calculos con el Scilab

 

//Calculos
aux=20*log10(1/6)
wc=10^(aux/20)
aux2=-90-45*log10(0.17/0.1)
mfase=180+aux2
aux3=-90-45*log10(0.2/0.1)
wcf=0.2*10^((180+aux3)/90)
aux4=aux-40*log10(wcf)
//comprobaciones
s=%s;
s1=s/(2*%pi)
g=2/(s+*(s+1)*(s+1));
gb=2/((s1+0.00000000001)*(s1+1)*(s1+2));
gbs=syslin('c',gb)
gs=syslin('c',g);
//margen de ganancia
[mg,fr]=g_margin(gbs/6)
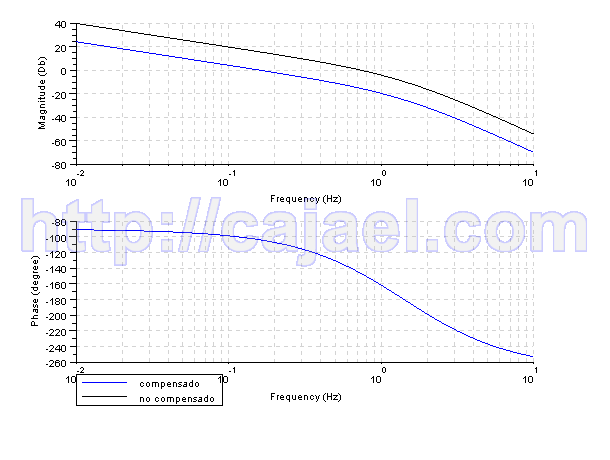
//Diagrama de Bode
clf;
bode([gbs;(gbs/6)],0.01,10,['compensado';'no compensado'])
//margen de fase
[pm,frp]=p_margin(gbs/6)

Image P2jun2008ss

 

Tags:

Español

Añadir nuevo comentario

Más información sobre los formatos de texto

Plain text

  • No se permiten etiquetas HTML.
  • Las direcciones de las páginas web y las de correo se convierten en enlaces automáticamente.
  • Saltos automáticos de líneas y de párrafos.
Pin It