Mensaje de error

  • Deprecated function: The each() function is deprecated. This message will be suppressed on further calls en book_prev() (línea 775 de /home1/montes/public_html/drupal/modules/book/book.module).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Deprecated function: implode(): Passing glue string after array is deprecated. Swap the parameters en drupal_get_feeds() (línea 394 de /home1/montes/public_html/drupal/includes/common.inc).

Cuestion 4 (Sistemas Discretos, sobreoscilacion, intervalo de pico y valor final)

Solapas principales

Enviado por pichu en Mar, 07/10/2012 - 13:26
Image 2008Jun1C4

 

SOLUCION:
La funcion de la salida sera:

 



 

Vamos a hacer la descomposicion de esta funcion en fracciones simples

 

\begin{displaymath}Y(z)=\frac{a}{z+0.1}+\frac{b}{z-0.4}+\frac{c}{z-1}\end{displaymath}

 

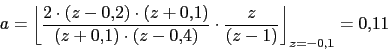
\begin{displaymath}a=\left\lfloor \frac{2\cdot (z-0.2)\cdot (z+0.1)}{(z+0.1)\cdot (z-0.4)}\cdot \frac{z}{(z-1)}\right\rfloor_{z=-0.1}=0.11\end{displaymath}

 

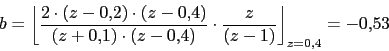
\begin{displaymath}b=\left\lfloor \frac{2\cdot (z-0.2)\cdot (z-0.4)}{(z+0.1)\cdot (z-0.4)}\cdot \frac{z}{(z-1)}\right\rfloor_{z=0.4}=-0.53\end{displaymath}

 

\begin{displaymath}c=\left\lfloor \frac{2\cdot (z-0.2)\cdot (z-1)}{(z+0.1)\cdot (z-0.4)}\cdot \frac{z}{(z-1)}\right\rfloor_{z=1}=2.42\end{displaymath}

 

 

 

Vamos a calcular la transfomada inversa Z de esta ecuacion.

 

\begin{displaymath}y(k)=0.11\cdot 0.1^{k-1}\cdot cos((k-1)\cdot \pi)-0.53\cdot 0.4^{k-1}+2.42\cdot 1^{k-1}\end{displaymath}



 

El valor final sera:

 

 

 

 

Vamos a calcular los valores de y en funcion de k.
k 0 1 2 3 4 5 6
y(k) 0 2 2.2 2.34 2.4106 2.4188 2.42

 

El intervalo de pico es 6.
El valor de sobreoscilacion es:

 

\begin{displaymath}M_{p}=\frac{2.42-2.42}{2.42}\cdot 100=0 \%\end{displaymath}

 

Calculos y comprobacion de resultados mediante el Scilab

clear;
z=%z;
g=2*(z-0.2)/((z+0.1)*(z-0.4));
r=z/(z-1);
gt=g*r
gs=syslin('d',g);
gts=syslin('d',gt);
//Calculo y comprobacion de descomposicion fraciones simples
a=horner((z+0.1)*gts,-0.1)
b=horner((z-0.4)*gts,0.4)
c=horner((z-1)*gts,1)
gt2=a/(z+0.1)+b/(z-0.4)+c/(z-1)
gf=tf2ss(gs);
se=pfss(gf)
//Calculo y comprobacion de la salida
for i=1:1:10
y(i)=a*0.1^(i-1)*cos((i-1)*%pi)+b*0.4^(i-1)+c*1^(i-1);
end;
aux=[0 y'];
k=0:1:40;
x=ones(1,41);
y2=flts(x,gs);
[aux;y2]
//Calculo del valor final y sobreoscilacion
aux2=horner(gs,1)
aux3=(max(y2)-aux2)/aux2
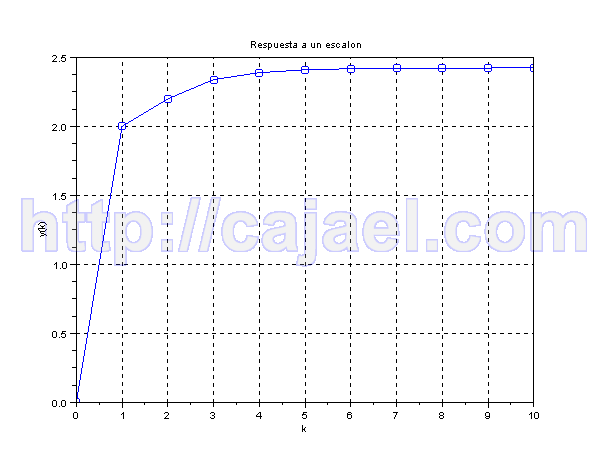
//Representacion grafica
clf;
plot(k,y2,'o');
plot(k,aux);
mtlb_axis([0 10 0 2.1]);
xgrid;
xtitle('Respuesta a un escalon','k','y(k)')
Image P4jun2008ps

 

Tags:

Español

Añadir nuevo comentario

Más información sobre los formatos de texto

Plain text

  • No se permiten etiquetas HTML.
  • Las direcciones de las páginas web y las de correo se convierten en enlaces automáticamente.
  • Saltos automáticos de líneas y de párrafos.
Pin It