[adsense:336x280:9156825571]
Vamos a dibujar el lugar de las raíces del sistema en lazo abierto y calcular las raíces en lazo cerrado cuando 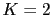
Programa en Scilab:
//Borramos la ventana grafica
clf;
//Declaramos la variable s y la funciones 'g','h' y 'g*h'
s=%s;
g=(s+1)/(s*(s^2+2*s+6));
h=1/(s+1);
gh=g*h;
//Declaramos la funcion g*h lineal y continua
ghs=syslin('c',gh)
//Declaramos ghs2 como la funcion anterior
pero con K=2
ghs2=2*ghs;
[adsense:336x280:9156825571]
//Calculamos las raices de (1+ghs2)*(s+1), este ultimo es el polo que se anulo
con el cero
glc=(1+ghs2)*(s+1);
r=roots(numer(glc))
//Dibujamos el lugar de las raices de la funcion ghs
evans(ghs);
mtlb_axis([-5 5 -5 5])
//Dibujamos el polo y el cero que se anularon:
plot(-1,0,'o');
plot(-1,0,'x');
//Dibujamos las raices para K=2;
plot(real(r),imag(r),'+');
xgrid;
xtitle('Lugar de las raices, los polos en lazo cerrado -> + para K=2','Eje real'
,'Eje imaginario');
Resultados
-->r=roots(numer(glc))
r =
- 0.3706383
- 1.
- 0.8146808 + 2.175406i
- 0.8146808 - 2.175406i
Comentarios recientes