Problema A.5.10 pag 304, Ogata

// Define s como Laplace
s=%s;

// Definimos la funcion de transferencia
num=5*(s+20);

den=s*(s+4.59)*(s^2+3.41*s+16.35);

// Hacemos un sistema lineal
g=syslin('c',num/den);

cr=g/. 1;

c=cr*(1/s);

// Hacemos la transformacion del sistema a espacio estado
cs=tf2ss(c);

// Hacemos la expansion en fracciones simples
fs=pfss(cs)
for k=1:3
clean(8*fs(k))
end;
 
  ans  =
 
    - 13.959394 + 3.0016262s     
    --------------------------   
                              2  
    10.011621 + 2.0004717s + s   
 ans  =
 
    - 46.040505 - 11.001626s     
    --------------------------   
                              2  
    9.9883925 + 5.9995283s + s   
 ans  =
 
    8   
    -   
    s  
    
     
-->c
 c  =
 
                 100 + 5s                 
    ----------------------------------    
                   2          3    4   5  
    100s + 80.0465s + 32.0019s + 8s + s

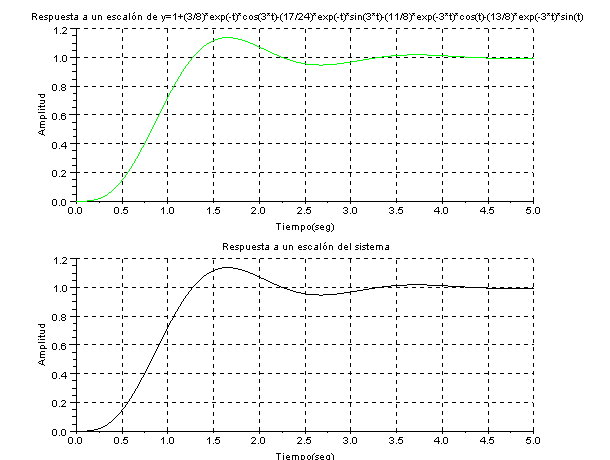
Vamos a dibujar la grafica segun la funcion de transferencia y segun la ecuacion en funcion del tiempo obtenida de la expansion en fracciones simples (programado en Scilab)