[adsense:responsibe:9545213979]
Mensaje de error
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Deprecated function: The each() function is deprecated. This message will be suppressed on further calls en book_prev() (línea 775 de /home1/montes/public_html/drupal/modules/book/book.module).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
- Deprecated function: implode(): Passing glue string after array is deprecated. Swap the parameters en drupal_get_feeds() (línea 394 de /home1/montes/public_html/drupal/includes/common.inc).
Se encuentra usted aquí
Problema A.5.9 pag 302, Ogata
Solapas principales
Vamos a hacer la expansion en fracciones simples con el Scilab del siguiente sistema:
Programa en Scilab:
![]()
Programa en Scilab
// Define s como Laplace
s=%s;
// Definimos la funcion de transferencia
num=80+72*s+25*s^2+3*s^3;
den=0+80*s+96*s^2+40*s^3+8*s^4+s^5;
// Hacemos un sistema lineal
sys_tf=syslin('c',num/den)
// Hacemos la transformacion del sistema a espacio estado
sys_ss=tf2ss(sys_tf);
// Hacemos la expansion en fracciones simples
tf=pfss(sys_ss);
for k=1:3
clean(tf(k))
end;
ans =
0.25 - 0.5625s
--------------
2
20 + 4s + s
ans =
1
-
s
ans =
- 1.25 - 0.4375s
--------------
2
4 + 4s + s
Con estas ecuaciones hacemo la expansion en fracciones simples
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Vamos a dibujar la grafica segun la funcion de transferencia y segun la ecuacion en funcion del tiempo obtenida de la expansion en fracciones simples (programado en Scilab)
Programa en Scilab:
// Define s como Laplace
s=%s;
// Definimos la funcion de transferencia
num=80+72*s+25*s^2+3*s^3;
den=80+96*s+40*s^2+8*s^3+s^4;
// Hacemos un sistema lineal
g=syslin('c',num/den);
//dibujamos el sistema
t=0:0.01:3;
gs=csim('step',t,g);
y=1-(9/16)*exp(-2*t).*cos(4*t)+(11/32)*exp(-2*t).*sin(4*t)-(7/16)*exp(-2*t)
-(6/16)*t.*exp(-2*t);
subplot(2,1,1);
xgrid;
xtitle('Respuesta a un escalon de 1-(9/16)*exp(-2*t)*cos(4*t)+(11/32)*exp(-2*t)
*sin(4*t)-(7/16)*exp(-2*t)-(6/16)*t*exp(-2*t)','Tiempo(seg)','Amplitud');
plot2d(t,y,3);
subplot(2,1,2);
plot2d(t,gs);
xgrid;
xtitle('Respuesta a un escalon del sistema','Tiempo(seg)','Amplitud')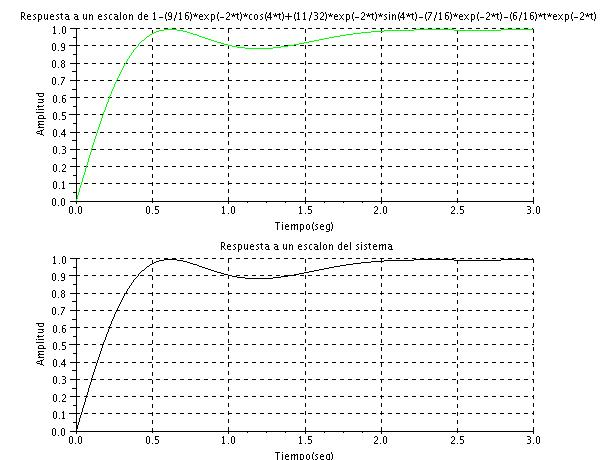
Español

Búsqueda personalizada
Idiomas
 English
English Español
Español
Comentarios recientes
- Muy bueno hace 10 años 1 mes
- good hace 10 años 1 mes
- Engranajes hace 10 años 2 meses
- REVISAR hace 10 años 2 meses
- UTIL hace 10 años 2 meses
- Realimentación hace 10 años 5 meses
- Hello There. I found your hace 10 años 6 meses
- Good web site! I really love hace 10 años 6 meses
- Well I really enjoyed reading hace 10 años 6 meses
- Thanks again for the blog hace 10 años 6 meses
Seguidores en Google
Busquedas populares
Inicio de sesión
Contenido popular
- 2.2.1 Calculo teorico variando RL
- Ejercicio 5.10 (Fuerza magnetica)
- Ejemplo 8-6 pag518 OGATA
- 1.4 Variar la frecuencia en el montaje practico del rectificador de media onda
- 4.6 Ejemplo
- Problema B2.3 pag51 OGATA 4ed(Tranformada de Laplace)
- 2006 Septiembre 2 semana
- SOFTWARE DE S.MECANICOS
- 2.2 Parte practica del circuito RC con potenciometro, desfase entre Ue e Uc
- 4.3 Ejemplo
- Apartada a) de la cuestion 3 EDiferenciales 1209S1 (Sistemas de ecuaciones diferenciales lineales homogeneos con coeficientes constantes, solucion general)
- 4.2 Simulacion estadistica del coeficiente de correlacion del Ejercicio 1.4
- 3.2 Calculo teórico de las curvas U-I del estabilizador de tensión
- 2.Simulacion estadistica del Ejercicio 4.2 (Esperanza,varianza,momentos centrados y no centrados)
- Curso basico de GeoGebra
- Practica 3. Pieza de chapa metalica en SolidWorks
- EXAMENES DE REGULACION
- Ejemplo 8-24 pag574 OGATA
- Representar el campo de vectores de una ecuacion diferencial de primer orden con SAGE
- Transformada Z con Scilab
- Apartada a) del Ejercicio 1 Campos y Ondas 1402S2 (Potencial electrico entre placas)
- 3.3 Simulacion estadistica del Coeficiente de variacion de Pearson del Ejercicio 1.3
- Apartada 1) del Ejercicio 1 Campos y Ondas 1309S1 (Potencial electrico; Campo electrico; Condiciones frontera)
- 3.2 Parte practica del circuito del cuadripolo pasivo
- Examenes 2007 RII
Páginas
Today's popular content
- 2010 Junio 2 semana
- 2010 Septiembre 1 semana
- 2010 Septiembre 2 semana
- Programa 5.3 pag 249, Ogata
- Programa 5.4 pag 250, Ogata
- Programa 5.5 pag 250, Ogata
- Programa 5.6 pag 252, Ogata
- Programa 5.8 pag 255, Ogata
- Programa 5.9 pag 256, Ogata
- Programa 5.10 pag 257, Ogata
- Programa 5.12 pag 260, Ogata
- Programa 5.14 pag 264, Ogata
- Programa 5.18 pag 274 con Scilab
- Ejemplo 5.13 pag 278, Ogata
- Problema A.5.8 pag 302, Ogata
- Problema A.5.9 pag 302, Ogata
- 2011 Septiembre 2 semana
- Problema A.5.10 pag 304, Ogata
- Problema A.5.11 pag 305, Ogata
- Problema A.5.12 pag 307, Ogata
- Problema A.5.13 pag 308, Ogata
- Problema A.5.14 pag 310, Ogata
- Problema A.5.15 pag 311, Ogata
- Problema A.5.16 pag 312, Ogata
- Problema A.5.23 pag 322, Ogata
Páginas
REGULACION AUTOMATICA
- APUNTES REGULACION
- CONTROL ADAPTATIVO
- Catalogos de Regulacion Automatica
- SIMULACIONES CON SCILAB
- Tranformada de Laplace
- Lugar de las Raices
- Respuesta Transitoria
- Programa 5.3 pag 249, Ogata
- Programa 5.4 pag 250, Ogata
- Programa 5.5 pag 250, Ogata
- Programa 5.6 pag 252, Ogata
- Programa 5.8 pag 255, Ogata
- Programa 5.9 pag 256, Ogata
- Programa 5.10 pag 257, Ogata
- Programa 5.12 pag 260, Ogata
- Programa 5.14 pag 264, Ogata
- Programa 5.18 pag 274 con Scilab
- Ejemplo 5.13 pag 278, Ogata
- Problema A.5.8 pag 302, Ogata
- Problema A.5.9 pag 302, Ogata
- Problema A.5.10 pag 304, Ogata
- Problema A.5.11 pag 305, Ogata
- Problema A.5.12 pag 307, Ogata
- Problema A.5.13 pag 308, Ogata
- Problema A.5.14 pag 310, Ogata
- Problema A.5.15 pag 311, Ogata
- Problema A.5.16 pag 312, Ogata
- Problema A.5.23 pag 322, Ogata
- Problema A.5.24 pag 323, Ogata
- Problema A.5.25 pag 324, Ogata
- Respuesta en Frecuencia con Scilab
- Transformada Z con Scilab
- EXAMENES DE REGULACION


Añadir nuevo comentario