Mensaje de error

Deprecated function: implode(): Passing glue string after array is deprecated. Swap the parameters en drupal_get_feeds() (línea 394 de /home1/montes/public_html/drupal/includes/common.inc).

poly

Español

Ejemplo 8-5 pag517 OGATA

Enviado por pichu en Mar, 06/19/2012 - 13:48
[adsense:336x280:9156825571]
Vamos a calcular el diagrama de Bode mediante el Scilab de la siguiente funcion:

 

Tags:

Español

Ejemplo 5.13 pag 278, Ogata

[adsense:336x280:9156825571]

Vamos a calcular Routh mediante Scilab del siguiente polinomio:

Polinomio

Programa en Scilab: 

h=poly([5 4 3 2 1],'s','coeff');

r=routh_t(h);

r




-->r

 r  =
 
    1.    3.    5.  
    2.    4.    0.  
    1.    5.    0.  
  - 6.    0.    0.  
    5.    0.    0.
Español

Programa 5.18 pag 274 con Scilab

Vamos a hacer la representacion grafica de la solucion del Ejemplo resuelto de la pagina 271 mediante Scilab:

 

Programa en Scilab:

num=poly([100 10 0],'s','coeff');

den=poly([100 10 1],'s','coeff');

t1=0:0.001:0.537;

t2=0.538:0.001:1.5;

x1=2.452*(t1^2);

x2=0.707*ones(t2);

y=syslin('c',num/den);

x=[x1 x2];

t=[t1 t2];

g=csim(x,t,y);

plot2d(t,-x,2);

plot2d(t,-g,5);

xgrid;

xtitle('Respuesta del sistema de resorte-masa-amortiguador colgado'
,'t(seg)','Entrada X negativa y salida Y negativa');

legends(['X','Y'],[2,5],opt=4);
Respuesta del sistema de resorte-masa-amortiguador colgado con Scilab

 

 

Español

Programa 5.14 pag 264, Ogata

Vamos a hacer la representacion grafica de la solucion del Ejemplo 5.9 que viene dada por una entrada escalon unitario al sistema(programado en Scilab):

 

Funcion de transferencia del sistema, Transformada de Laplace

 

Programa en Scilab:
num=poly([0 0.35 0.1],'s','coeff');

den=poly([2 3 1],'s','coeff');

t=0:0.1:7;

g=syslin('c',num/den);

gs=csim('step',t,g);

plot(t,gs);

xgrid;

xtitle('respuesta a un Escalon unitario de G(s)=(0.1s^2+0.35s)/(s^2+3s+2)'
,'t(seg)','Amplitud')

 

Respuesta a un escalon unitario del sistema con Scilab

Como se ve la funcion sale del 0 cuando tendria que salir del 0.1 vamos a repetir el programa pero utilizando en vez de una entrada escalon para

$G(s)=\frac{(0.1\cdot s^{2}+0.35 \cdot s)}{(s^{2}+3\cdot s+2)}$, una entrada impulso para el sistema

Funcion de transferencia para un sistema equivalente con entrada impulos, es decir, lo mismo. Si nos fijamos al ejecutar el codigo anterior de Scilab, el sistema nos da un warning despues de ejecutar el csim.

 

Programa en Scilab:
num=poly([0 0.35 0.1 0],'s','coeff');

den=poly([0 2 3 1],'s','coeff');

t=0:0.1:7;

g=syslin('c',num/den);

gs=csim('impulse',t,g);

plot2d(t,gs,2);

xgrid;

xtitle('respuesta a un impulso unitario de G(s)=(0.1s^2+0.35s)/(s^3+3s^2+2s)'
,'t(seg)','Amplitud');

 

Respuesta del sistema equivalente a un impulso con Scilab
Español

Programa 5.12 pag 260, Ogata

Vamos a hacer la representacion grafica de la respuesta a una entrada rampa unitaria al siguiente sistema(programado en Scilab):

 

Funcion de transferencia de segundo orden, Transformada de Laplace


 

Programa en Scilab (es como el programa 5.10 pero cambia la entrada y como introducimos el sistema):
num=poly([1 0 0],'s','coeff');

den=poly([1 1 1],'s','coeff');

t=0:0.1:7;

g=syslin('c',num/den);

gs=csim(t,t,g);

plot(t,gs,'+');

plot2d(t,t)

xgrid;

xtitle('respuesta a una rampa unitaria de G(s)=1/(s^2+s+1)','t(seg)'
,'Entrada y salida');

xstring(1.8,3,'Entrada');

xstring(4.4,3,'Salida');
Respuesta del sistema a una rampa unitaria con Scilab
Español

Programa 5.10 pag 257, Ogata

Vamos a hacer la representacion grafica de la respuesta a una entrada rampa unitaria al siguiente sistema(programado en Scilab):

 

Funcion de transferencia de segundo orden, Transformada de Laplace


Programa en Scilab:
num=poly([1 0 0 0],'s','coeff');

den=poly([0 1 1 1],'s','coeff');

t=0:0.1:7;

g=syslin('c',num/den);

gs=csim('step',t,g);

plot(t,gs,'+');

plot2d(t,t);

xgrid;

xtitle('respuesta a una rampa unitaria de G(s)=1/(s^2+s+1)','t(seg)'
,'Entrada y salida');

xstring(1.8,3,'Entrada');

xstring(4.4,3,'Salida');

 

Respuesta del sistema a una rampa unitaria con Scilab

 

Español

Programa 5.9 pag 256, Ogata

Vamos a hacer la representacion grafica de la respuesta a una entrada escalon unitario al siguiente sistema, obteniendo la misma respuesta que en Programa 5.8 (programado en Scilab):

 

Funcion de transferencia, Transformada de Laplace

 

Programa en Scilab:

num=poly([1 0 0],'s','coeff');

den=poly([1 0.2 1],'s','coeff');

t=0:0.1:70;

g=syslin('c',num/den);

gs=csim('impulse',t,g);

plot2d(t,gs);

xgrid;

xtitle('respuesta a un impulso unitario de G(s)=1/(s^2+0.2s+1)');
Respuesta al sistema a un impulso con Scilab
Español

Programa 5.8 pag 255, Ogata

Vamos a hacer la representacion grafica de la respuesta a una entrada impulso unitario al siguiente sistema (programado en Scilab):

 

Funcion de transferencia de segundo orden, Transformada de Laplace


Programa en Scilab:
num=poly([1 0 0],'s','coeff');

den=poly([1 0.2 1],'s','coeff');

t=0:0.1:70;

g=syslin('c',num/den);

gs=csim('impulse',t,g);

plot2d(t,gs);

xgrid;

xtitle('respuesta a un impulso unitario de G(s)=1/(s^2+0.2s+1)');

 

Respuesta del sistema a un impulso unitario con Scilab

Español

Programa 5.6 pag 252, Ogata

Vamos a calcular el tiempo de subid, tiempo de pico, maxima sobreelongacion y tiempo de asentamiento utilizando el Scilab del siguiente sistema:

 

Funcion de transferencia de segundo orden, Transformada de Laplace


Programa en Scilab: 
num=poly([25 0 0],'s','coeff');

den=poly([25 6 1],'s','coeff');

t=0:0.005:5;

g=syslin('c',num/den);

gs=csim('step',t,g);

r=1;

while gs(r)<1.0001;

r=r+1;

end;
tiemposubida=(r-1)*0.005;

[gsmax,rp]=max(gs);

tiempopico=(rp-1)*0.005;

ElongacionMax=gsmax-1;

rmax=5/0.005;

k=rmax+1;

while gs(k)>0.98 & gs(k)<1.02;
k=k-1;
end;

-->tiemposubida
 tiemposubida  =
 
    0.555  
 
-->tiempopico
 tiempopico  =
 
    0.785  
 
-->ElongacionMax
 ElongacionMax  =
 
    0.0947800  
 
-->tiempoasentamiento
 tiempoasentamiento  =
 
    1.185

 

Español

Programa 5.5 pag 250, Ogata

[adsense:336x280:9156825571]
Vamos a hacer la representacion grafica de la respuesta a una entrada escalon unitario, dando a el factor
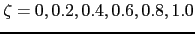
de amortiguacion los siguientes valores del sistema:$\zeta=0, 0.2, 0.4, 0.6, 0.8, 1.0 $
Funcion de tranferencia con el factor de amortiguacion, Transformada de Laplace

 

Programa en Scilab:
t=0:0.2:10;

zeta=[0 0.2 0.4 0.6 0.8 1];

cv=[1 2 3 4 5 6];

for n=1:6

num=poly([1 0 0],'s','coeff');

den=poly([1 2*zeta(n) 1],'s','coeff');

g=syslin('c',num/den);

gs=csim('step',t,g);

plot2d(t,gs,style=cv(n))

end;

xgrid;

xtitle('Representacion a un escalon unitario con wn=1,zeta=0 , 0.2
, 0.4,0.6,0.8,1','t(seg)','Respuesta');

legends(['zeta=0','zeta=0.2','zeta=0.4','zeta=0.6','zeta=0.8','zeta=1']
,[1,2,3,4,5,6],opt=4);
Respuesta del sistema a un escalor para varios valores del factor de amortiguamiento con Scilab

 

Español

Páginas
Pin It
Subscribe to RSS - poly