[adsense:responsibe:9545213979]
Problema 1 (Lugar de las raices, PID, compensador de adelanto)
Solapas principales

Solucion:
Apartado 1 (Dibujar el lugar de las raices del sistema sin compensar)
-
Polos y ceros
Polos: p1=-1,
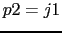 y
y 
Ceros: c1=-2
ramas en el infinito: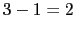
-
Lugar del las raices en el eje real
Entre -1 y
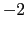
-
Asintotas
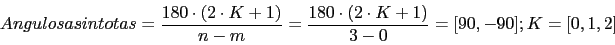 Punto de cruce de las asintotas en el eje real
Punto de cruce de las asintotas en el eje real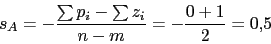
-
Angulo de salida en
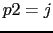
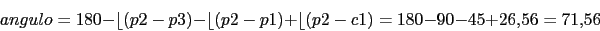 Representacion del lugar de las raices
Representacion del lugar de las raices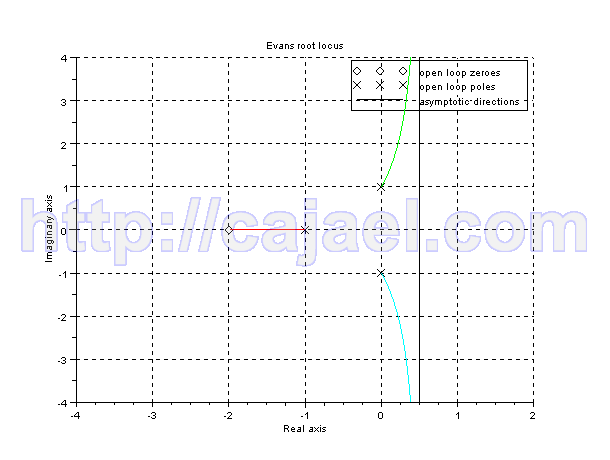
Apartado 2 (Indicar el angulo que debe aportar el regulador)
![]()
![]()
![]()
![]()
![]()
![]()
Con lo que tenemos los datos del polo dominante que queremos para el sistema
![]()
Vamos a calcular el angulo de fase del sistema para s1
![]()
Para conseguir 180 usaremos una red de adelanto. El angulo que tiene que aportar el compensador es de:
![]()
Apartado 3 (Diseñar el regulador)
Vamos a necesitar un regulador de adelanto
![]()
Como el maximo valor que puede aportar un cero es el situado en el 0 y nos da un valor de angulo de 126.23. Tendremos que utilizar por lo menos 2 ceros. Con lo que tendriamos que utilizar dos compensadores en serie.Uno de ellos podria ser el siguiente y asi simplificamos la funcion de transferencia resultante.
![]()
![]()
Con lo que el angulo para el otro compensador nos quedaria:
![]()
Nos es valido es menor que ![]() .
.
Como vamos a tener que meter una red de atraso podemos intentar hacer coincidir el cero del segundo compensador de adelanto con el cero de la red de atraso para cumplir ![]() . Vamos entonces a calcular la red de atraso:
. Vamos entonces a calcular la red de atraso:
Red de atraso para que la ![]() sea
sea ![]()
![]()
![]()
Como vemos la red de atraso tiene que tener polo en el cero para verificar ![]()
![]()
Podemos intentar un PID. Asi no tendriamos que meter el segundo compensador de adelanto
![]()
![]()
![]()
![]()
Nos vale es menor que ![]()
![]()
![]()
![]()
Con lo que el PID nos quedaria
![]()
El compensador adelanto-PID nos quedaria
![]()
Vamos a calcular la 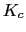
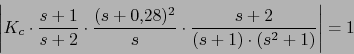
![]()
El compensador sera:
![]()
Apartado 4 (Dibujar el lugar de las raices del sistema compensado)
![]()
-
Polos y ceros
Polos: p1=0,
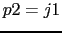 y
y 
Ceros: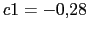 ,
,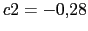
ramas en el infinito: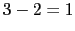
-
Asintotas Asintota en 180
-
Lugar del las raices en el eje real
Entre 0 y
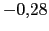 y entre
y entre 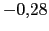 y
y 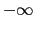
-
Puntos de ruptura y de ingreso
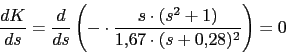 Un pto de ingreso en -1.59
Un pto de ingreso en -1.59 -
Angulo de salida en
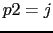
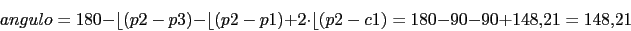 Representacion del lugar de las raices
Representacion del lugar de las raices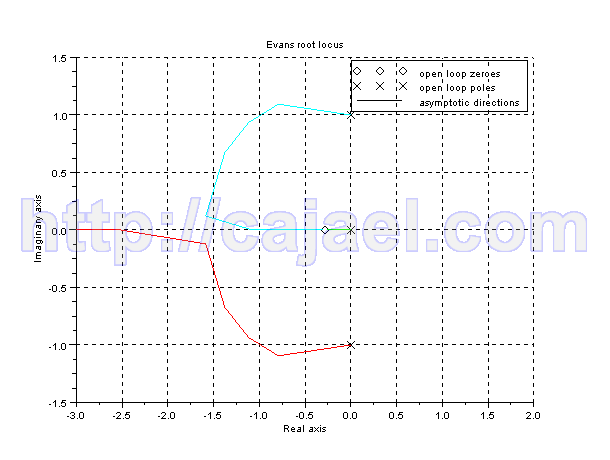
Calculos y comprobaciones con el Scilab
s=%s;
g=(s+2)/((s+1)*(s^2+1));
gs=syslin('c',g);
//Calculo de los polos de g
p=roots(denom(gs))
c=roots(numer(gs));
//Asintotas
for i=0:1
aas=180*(2*i+1)/2
end;
sas=(p(1)+p(2)+p(3)-c(1))/2
//Lugar de las raices de g
clf;
evans(gs)
xgrid;
mtlb_axis([-4 2 -4 4]);
//Calculo de el polo dominante ts=5;
mp=0.1;
sig=4/ts;
wd=-%pi*sig/log(mp)
s1=-sig+%i*wd;
//Angulo del sistema en s1
gs1=horner(gs,s1);
angsgs1=atan(imag(gs1),real(gs1));
auxgs1=360*angsgs1/(2*%pi)
//Angulo total del compensador de adelanto
angc=180-aux
//Angulo de s1
auxangs1=atan(imag(s1),real(s1));
angs1=360*auxangs1/(2*%pi)
//Angulo de compensador adelanto 1 en s1
gc1=(s+1)/(s+2)
gc1s1=horner(gc1,s1);
agc1s1=atan(imag(gc1s1),real(gc1s1));
auxgc1s1=360*agc1s1/(2*%pi)
//Angulo para el otro compensador de adelanto
agc2=angc-auxgc1s1
//Angulo ceros PID
acpids=agc2+angs1
acpid=acpids/2
axacpid=2*%pi*acpid/360
//Cero del PID
a2=-real(s1)-(imag(s1)/tan(%pi-axacpid))
//Calculo del PID
gc2=(s+a2)^2/s
//Compensador sin la Kc
gc=gc1*gc2
//Vamos a calcular la Kc del compensador
gt=gc*g;
gts=syslin('c',gt);
aux3=abs(horner(gt,s1));
kc=1/aux3
//Vamos a comprobar que el resultado esta bien
gt2=kc*gt;
gcgs1=horner(gt2,s1)
gt2s=syslin('c',gt2);
//Calculo de los polos de gt
pt=roots(denom(gt2s))
ct=roots(numer(gt2s))
//Angulo de la asintota de gt
angast=(pt(1)+pt(2)+pt(3)-2*ct(1))/3
//Calculo de la derivada, para ptos ingreso de gt
dk=derivat(-1/gt2s)
ptsingreso=roots(numer(dk))
//Lugar de las raices de gt
clf;
evans(gt2s)
xgrid;
mtlb_axis([-3 2 -1.5 1.5]);
//respuesta a un escalon de todo el sistema
glc=gt2/. 1 ;
glcs=syslin('c',glc);
t=0:0.1:200;
y=csim('step',t,glcs);
clf
subplot(2,1,1);
xgrid;
plot(t,y)
xtitle('Respuesta a un escalon','t','y(t)')
subplot(2,1,2);
t2=0:0.1:20;
y2=csim('step',t2,glcs);
xgrid;
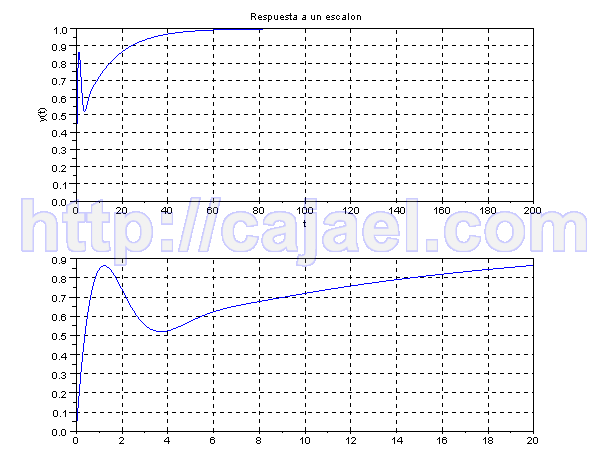
plot(t2,y2)
Respuesta de todo el sistema a un escalon
Español



Añadir nuevo comentario