Mensaje de error

  • Deprecated function: The each() function is deprecated. This message will be suppressed on further calls en book_prev() (línea 775 de /home1/montes/public_html/drupal/modules/book/book.module).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Deprecated function: implode(): Passing glue string after array is deprecated. Swap the parameters en drupal_get_feeds() (línea 394 de /home1/montes/public_html/drupal/includes/common.inc).

Problema 1 (Lugar de las raices, error de posicion)

Solapas principales

Enviado por pichu en Sáb, 07/14/2012 - 21:45

Image 2008Sept2P

SOLUCION:

Apartado 1 (Dibujar el lugar de las raices del sistema sin compensar)

  • Polos y ceros

    Polos: 0,

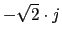    $-\sqrt{2}\cdot j$ y

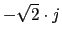
    $-\sqrt{2}\cdot j$
    Ceros: Ninguno

  • Lugar del las raices en el eje real

    A la izquierda del polo en cero
  • Asintotas

    \begin{displaymath}Angulos asintotas =\frac{180\cdot (2\cdot K+1)}{n-m}=\frac{180\cdot (2\cdot K+1)}{3-0}=[60 ,-180, -60]\end{displaymath}


    \begin{displaymath}K=[0 ,1 ,2]\end{displaymath}


    Punto de cruce de las asintotas en el eje real

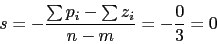
    \begin{displaymath}s=-\frac{\sum{p_{i}}-\sum{z_{i}}}{n-m}=-\frac{0}{3}=0\end{displaymath}

  • Angulos de salida del lugar de las raices en los polos

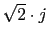    $\sqrt{2}\cdot j$ y

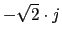
    $-\sqrt{2}\cdot j$

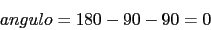    \begin{displaymath}angulo=180-90-90=0\end{displaymath}


    Con lo que el lugar de las raices nos queda dibujado mediante el Scilab:
    s=%s;
g=1/(s*(s^2+2));
gs=syslin('c',g);
clf;
evans(gs);
xgrid;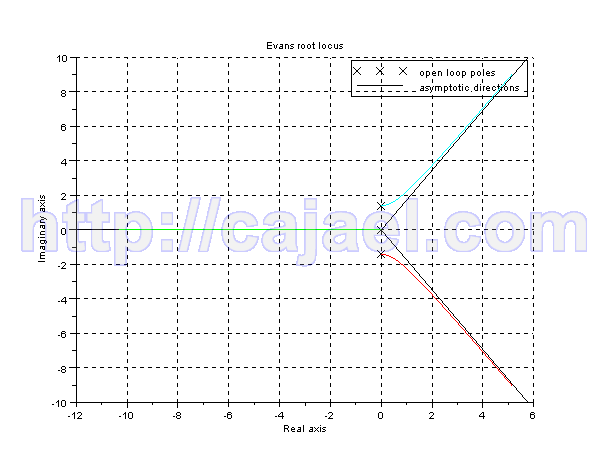

    Image P1sept2008ss

Apartado 2 (Indicar el angulo que debe aportar la red de adelanto)

\begin{displaymath}M_{p}=100\cdot e^{- \frac{\pi \cdot \sigma}{w_{d}}}\leq 10 \end{displaymath}


\begin{displaymath}t_{s}=\frac{4}{\sigma} \leq 10\end{displaymath}


\begin{displaymath}\sigma=\frac{4}{10}=0.4\end{displaymath}


\begin{displaymath}- \frac{\pi \cdot 0.4}{w_{d}}=ln(0.1)\end{displaymath}


\begin{displaymath}- \frac{\pi \cdot 0.4}{ln(0.1)}=w_{d}\end{displaymath}


\begin{displaymath}w_{d}=0.546\end{displaymath}


Con lo que tenemos los datos del polo dominante que queremos para el sistema

\begin{displaymath}s1=-\sigma+j\cdot w_{d}=-0.4+j\cdot 0.546\end{displaymath}


Vamos a calcular la fase del sistema para este valor

\begin{displaymath}\lfloor{G(s1)}=\lfloor{\frac{1}{s1\cdot (s1^{2}+2)}}=\end{displaymath}


 

\begin{displaymath}=\lfloor{\frac{1}{(-0.4+j\cdot 0.546)\cdot (-0.4+j\cdot 0.546-j\cdot \sqrt{2})\cdot (-0.4+j\cdot 0.546+j\cdot \sqrt{2})}}=\end{displaymath}


\begin{displaymath}=\lfloor{\frac{1}{(-0.4+j\cdot 0.546)\cdot (-0.4-j\cdot 0.868)\cdot (-0.4+j\cdot 1.96)}}=\end{displaymath}


\begin{displaymath}=-(180-atan(\frac{0.546}{0.4}))-(180+atan(\frac{0.868}{0.4}))-(180-atan(\frac{1.96}{0.4}))=-113\end{displaymath}


Para conseguir 180 mediante una red de adelanto se tendra que sumar:

\begin{displaymath}angulocompensador=113+180=293.01\end{displaymath}

 

Como el angulo a compensar no es aconsejable que sea superior a 65, pondremos cinco compensadores iguales en serie:

\begin{displaymath}angulocompensador=\frac{293.01}{5}=58.6\end{displaymath}


Apartado 3 (Vamos a diseñar la red de adelanto)

Vamos a poner el cero del compensador en 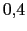$0.4$

\begin{displaymath}\lfloor{\frac{(s1+0.4)}{(s1+b)}}=\lfloor{\frac{(-0.4+j\cdot 0.546+0.4)}{(-0.4+j\cdot 0.546+b)}}=58.6\end{displaymath}


\begin{displaymath}90-atan(\frac{0.546}{b-0.4})=58.6\end{displaymath}


\begin{displaymath}90-58.6=31.4=atan(\frac{0.546}{b-0.4})\end{displaymath}


\begin{displaymath}tg(31.4)=\frac{0.546}{b-0.4}\end{displaymath}


\begin{displaymath}b-0.4=\frac{0.546}{tg(31.4)}\end{displaymath}


\begin{displaymath}b=0.4+\frac{0.546}{tg(31.4)}=1.29\end{displaymath}


Con lo que el compensador nos queda:

\begin{displaymath}G_{c}(s)=K_{c}\cdot \frac{(s+0.4)^{5}}{(s+1.29)^{5}}\end{displaymath}


 

Ahora vamos a calcular la 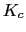$K_{c}$

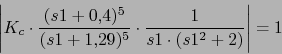
\begin{displaymath}\left\vert K_{c}\cdot \frac{(s1+0.4)^{5}}{(s1+1.29)^{5}}\cdot \frac{1}{s1\cdot (s1^{2}+2)} \right\vert =1\end{displaymath}


\begin{displaymath}K_{c}=33.1\end{displaymath}


El compensador sera:

\begin{displaymath}G_{c}(s)=33.1\cdot \frac{(s+0.4)^{5}}{(s+1.29)^{5}}\end{displaymath}


 

Vamos a hacer la comprobacion mediante el Scilab de que el sistema compensado cumple los requisitos.
s=%s;
g=1/(s*(s^2+2));
gs=syslin('c',g);
ts=10;
mp=0.1
sig=4/ts;
wd=-%pi*sig/log(mp)
s1=-sig+%i*wd;
gs1=horner(gs,s1);
anggs1=atan(imag(gs1),real(gs1))
aux=360*anggs1/(2*%pi);
angc=180+113;
angc1=angc/5;
a=0.4;
b=a+0.546/tan((90-angc1)*2*%pi/360)
gc=(s+a)^5/(s+b)^5;
gt=gc*g;
gts=syslin('c',gt);
aux2=abs(horner(gt,s1));
kc=1/aux2;
gt2=kc*gt;
gcgs1=horner(gt2,s1)

El valor de

$G_{c}(s1)\cdot G(s1)=-1$

 gcgs1 =
 
 - 1.0000000 - 0.0002514i

Apartado 4 (Dibujar el lugar de las raices del sistema compensado)

\begin{displaymath}G_{c}(s)\cdot G(s)=33.1\cdot \frac{(s+0.4)^{5}}{(s+1.29)^{5}} \cdot \frac{1}{s\cdot (s^{2}+2)} \end{displaymath}


  • Polos y ceros

    Polos: 5 polos en 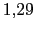$1.29$,1 en 0,

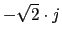    $-\sqrt{2}\cdot j$ y

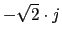
    $-\sqrt{2}\cdot j$
    Ceros: 5 ceros en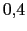 $0.4$

  • ramas

    3 ramas al infinito
  • Lugar del las raices en el eje real

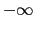
    Entre 0 y -0.4, de -1.29 a el $-\infty$
  • Asintotas

    \begin{displaymath}Angulos asintotas =\frac{180\cdot (2\cdot K+1)}{n-m}=\frac{180\cdot (2\cdot K+1)}{8-5}=[60 ,-180, -60];K=[0 ,1 ,2]\end{displaymath}


    Punto de cruce de las asintotas en el eje real

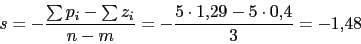
    \begin{displaymath}s=-\frac{\sum{p_{i}}-\sum{z_{i}}}{n-m}=-\frac{5\cdot 1.29-5\cdot 0.4}{3}=-1.48\end{displaymath}

  • Angulos de salida del lugar de las raices en los polos

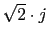    $\sqrt{2}\cdot j$ y

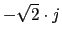
    $-\sqrt{2}\cdot j$

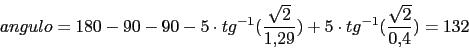
    \begin{displaymath}angulo=180-90-90-5\cdot tg^{-1}(\frac{\sqrt{2}}{1.29})+5\cdot tg^{-1}(\frac{\sqrt{2}}{0.4})=132\end{displaymath}



     

  • Ptos de ruptura e ingreso En el 0.4 y el 1.29

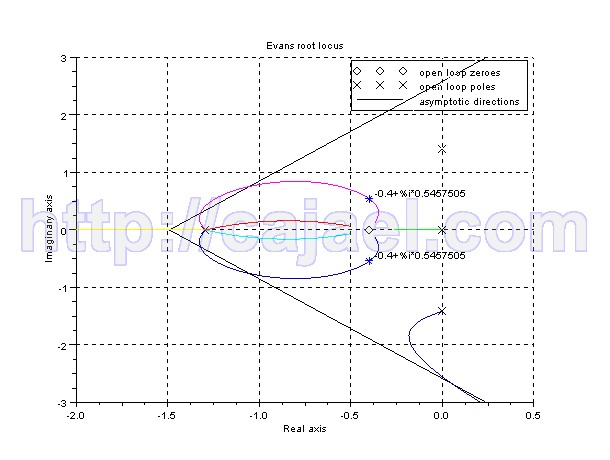
Con lo que el lugar de las raices nos queda dibujado mediante el Scilab

 

s=%s;
g=1/(s*(s^2+2));
gs=syslin('c',g);
ts=10;
mp=0.1
sig=4/ts;
wd=-%pi*sig/log(mp)
s1=-sig+%i*wd;
gs1=horner(gs,s1);
anggs1=atan(imag(gs1),real(gs1))
aux=360*anggs1/(2*%pi);
angc=180+113;
angc1=angc/5;
a=0.4;
b=a+0.546/tan((90-angc1)*2*%pi/360)
gc=(s+a)^5/(s+b)^5;
gt=gc*g;
gts=syslin('c',gt);
aux2=abs(horner(gt,s1));
kc=1/aux2;
gt2=kc*gt;
clf;
evans(gt2)
mtlb_axis([-2 0.25 -3 3])
xgrid
plot(real(s1),imag(s1),'*')
plot(real(s1),-imag(s1),'*')
aux3=string(real(s1)+%i*imag(s1))
aux4=string(real(s1)+%i*imag(s1))
xstring(real(s1),imag(s1),aux3)
xstring(real(s1),-imag(s1),aux4)

Image P1sept2008ssb

Apartado 5 (Vamos a calcular el Error de posicion)



\begin{displaymath}e_{p}=\frac{1}{\infty}=0\end{displaymath}


 

Tags:

Español

Añadir nuevo comentario

Más información sobre los formatos de texto

Plain text

  • No se permiten etiquetas HTML.
  • Las direcciones de las páginas web y las de correo se convierten en enlaces automáticamente.
  • Saltos automáticos de líneas y de párrafos.
Pin It