Mensaje de error

  • Deprecated function: The each() function is deprecated. This message will be suppressed on further calls en book_prev() (línea 775 de /home1/montes/public_html/drupal/modules/book/book.module).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Deprecated function: implode(): Passing glue string after array is deprecated. Swap the parameters en drupal_get_feeds() (línea 394 de /home1/montes/public_html/drupal/includes/common.inc).

Problema 1 (Bode, compensador de adelanto, error de velocidad, margen de fase y margen de ganancia)

Solapas principales

Enviado por pichu en Mié, 07/11/2012 - 12:57
Image 2008Jun2P
SOLUCION:

Apartado 1 (Dibujar los diagramas de Bode)

w 0.05   0.2   0.5   2   5   20
$\frac{1}{s}$ -90 (0) -90 (0) -90 (0) -90 (0) -90 (0) -90
$2\cdot s+1$ 0 (45)   (45) 45 (45) 72 (45) 90 (0) 90

$\frac{1}{(\frac{s}{2})^{2}+0.05\cdot \frac{s}{2} +1}$

 0 (0) 0 (0) 0 () -90 () -180 (0) -180
  -90 (45)   (45) -45   -107   -180 (0) -180

 

\begin{displaymath}45\cdot log(\frac{2}{0.05})=72\end{displaymath}

  • Vamos a calcular la K para que verifique la constante de error de velocidad

     

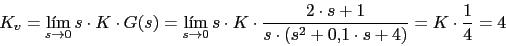
    \begin{displaymath}K_{v}=\lim_{s \rightarrow 0}{s\cdot K \cdot G(s)}=\lim_{s \ri...<br /> ...\cdot s+1}{s\cdot (s^{2}+0.1\cdot s +4)}}=K\cdot \frac{1}{4}= 4\end{displaymath}


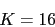
    \begin{displaymath}K=16\end{displaymath}



     

  • Vamos a calcular el diagrama de Bode para la funcion

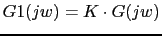
    $G1(jw)=K\cdot G(jw)$

     

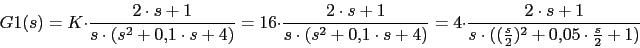
    \begin{displaymath}G1(s)=K\cdot \frac{2\cdot s+1}{s\cdot (s^{2}+0.1\cdot s +4)}=...


    Las ganancias: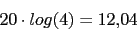

    \begin{displaymath}20\cdot log(4)=12.04\end{displaymath}


     

    w   0.5   2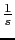  
    $\frac{1}{s}$ (-20)   (-20)   (-20)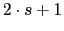
    $2\cdot s+1$ (0)   (20)   (20)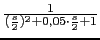

    $\frac{1}{(\frac{s}{2})^{2}+0.05\cdot \frac{s}{2} +1}$

    		 (0)   (0)   (-40)
      (-20) 18.06 (0) 18.06 (-40)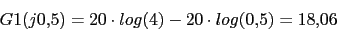

     

    \begin{displaymath}G1(j0.5)=20\cdot log(4)-20\cdot log(0.5)=18.06\end{displaymath}


    Al calcular las fases tenemos que tener cuidado porque en: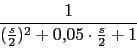

    \begin{displa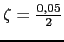ymath}\frac{1}{(\frac{s}{2})^{2}+0.05\cdot \frac{s}{2} +1}\end{displaymath}


    La

    $\zeta=\frac{0.05}{2}$ esta muy proxima a 0 lo que implica: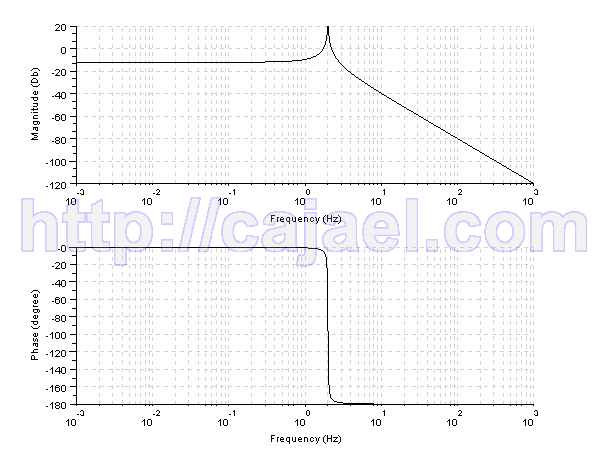

    Image P1jun2008ss


Apartado 2 (Realizar el diseño del regulador)

  • Ahora vamos a calcular el margen de fase del sistema. Primero calcularemos la frecuencia de cruce de ganancia

     

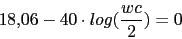
    \begin{displaymath}18.06-40\cdot log(\frac{wc}{2})=0\end{displaymath}


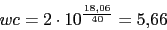
    \begin{displaymath}wc=2\cdot 10^{\frac{18.06}{40}}=5.66\end{displaymath}


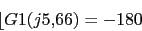
    \begin{displaymath}\lfloor{G1(j5.66)}=-180\end{displaymath}


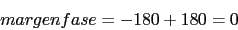
    \begin{displaymath}margenfase=-180+180=0\end{displaymath}


     

  • Como el margen de fase que necesitamos es 50. Vamos a utilizar un compensador de adelanto. Vamos a calcularlo

     

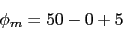
    \begin{displaymath}\phi_{m}=50-0+5\end{displaymath}


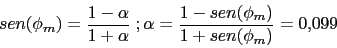    \begin{displaymath}sen(\phi_{m})=\frac{1-\alpha}{1+\alpha}\; ; \alpha=\frac{1-sen(\phi_{m})}{1+sen(\phi_{m})}=0.099\end{displaymath}


     

    Vamos a calcular la nueva frecuencia de cruce de ganancia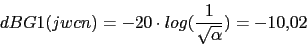

    \begin{displaymath}dBG1(jwcn)=-20\cdot log(\frac{1}{\sqrt{\alpha}})=-10.02\end{displaymath}


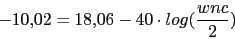
    \begin{displaymath}-10.02=18.06-40\cdot log(\frac{wnc}{2})\end{displaymath}


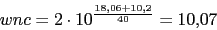
    \begin{displaymath}wnc=2\cdot 10^{\frac{18.06+10.2}{40}}=10.07\end{displaymath}


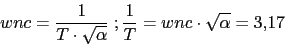    \begin{displaymath}wnc=\frac{1}{T\cdot \sqrt{\alpha}}\; ; \frac{1}{T}=wnc\cdot \sqrt{\alpha}=3.17\end{displaymath}


     

    Con lo que el compensador nos quedaria asi:

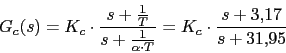    \begin{displaymath}G_{c}(s)=K_{c}\cdot \frac{s+\frac{1}{T}}{s+\frac{1}{\alpha \cdot T}}=K_{c}\cdot\frac{s+3.17}{s+31.95}\end{displaymath}


     

    Vamos a calcular la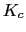 $K_{c}$

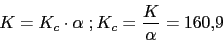
    \begin{displaymath}K=K_{c}\cdot \alpha \; ; K_{c}=\frac{K}{\alpha}=160.9\end{displaymath}


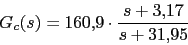
    \begin{displaymath}G_{c}(s)=160.9\cdot \frac{s+3.17}{s+31.95}\end{displaymath}


     

  • Vamos a comprobar que verifica las especificaciones

     

    w 2   3.17   31.95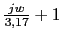  

    $\frac{jw}{3.17}+1$

    		 0 (0) 0 (20)   (-20)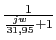

    $\frac{1}{\frac{jw}{31.95}+1}$

    		 0 (0) 0 (0)   (20)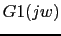
    $G1(jw)$ 18.06 (-40) 10.05 (-40)   (-40)
      18.06 (-40) 10.05 (-20) -10 (-40)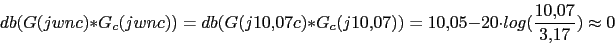

     

    \begin{displaymath}db(G(jwnc)*G_{c}(jwnc))=db(G(j10.07c)*G_{c}(j10.07))=10.05-20\cdot log(\frac{10.07}{3.17})\approx 0\end{displaymath}


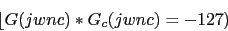
    \begin{displaymath}\lfloor{G(jwnc)*G_{c}(jwnc)}=-127)\end{displaymath}


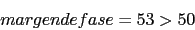
    \begin{displaymath}margen de fase=53>50\end{displaymath}


     

    w 0.317   3.17   3.195   31.7   31.95   319.5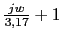

    $\frac{jw}{3.17}+1$

    		0 (45) 45 (45) 45 (45) 90 (0) 90 (0) 90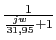

    $\frac{1}{\frac{jw}{31.95}+1}$

    		 0 (0) 0 (0) 0 (-45) -45 (-45) -45 (-45) -90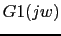
    $G1(jw)$   ()   ()   () -180 (0) -180 (0) -180
        ()   ()   () -135 (-45) -135 (-45) -180

    El cruce con -180 es en el infinito. Con lo que el margen de ganancia es infinito. Por lo tanto verifica las condiciones.

     

Calculos y representacion con el Scilab

s=%s;
s1=s/(2*%pi)
aux=1/(s1^2+0.05*s1+4)
aux2=syslin('c',aux);
clf;
bode(aux2)
aux3=20*log10(4)
g1_0_5=aux3-20*log10(0.5)
wc=2*10^(g1_0_5/40)
clg=(2*s+1)/(s*(s^2+0.1*s+4))
gs=syslin('c',g);
g1=16*g;
g1s=syslin('c',g1)
gb1=16*(2*s1+1)/(s1*(s1^2+0.1*s1+4))
gb1s=syslin('c',gb1)
clf;
bode(gb1s)
aux4=horner(g1s,%i*wc);
aux5=20*log10(abs(aux4))
aux6=atan(imag(aux4),real(aux4));
aux7=360*aux6/(2*%pi)
phm=50+5;
aux8=2*%pi*phm/360;
aux9=sin(aux8);
alp=(1-aux9)/(1+aux9)
g1wnc=-20*log10(1/sqrt(alp))
wnc=2*10^((g1_0_5-g1wnc)/40)
a=wnc*sqrt(alp)
b=a/alp
kc=16/alp
gc=kc*(s+a)/(s+b)
gt=g*gc;
gts=syslin('c',gt)
aux10=horner(gts,%i*wnc)
aux11=20*log10(abs(aux10))
aux12=atan(imag(aux10),real(aux10));
aux13=360*aux12/(2*%pi)
aux14=aux13+180
g1_317=g1_0_5-40*log10(3.17/2)
aux15=g1_317-20*log10(10.07/3.17)
kv=horner(s*gts,0)
gcb=kc*(s1+a)/(s1+b)
gb=(2*s1+1)/(s1*(s1^2+0.1*s1+4))
gtb=gb*gcb;
gbs=syslin('c',gb);
gcbs=syslin('c',gcb);
gtbs=syslin('c',gtb);
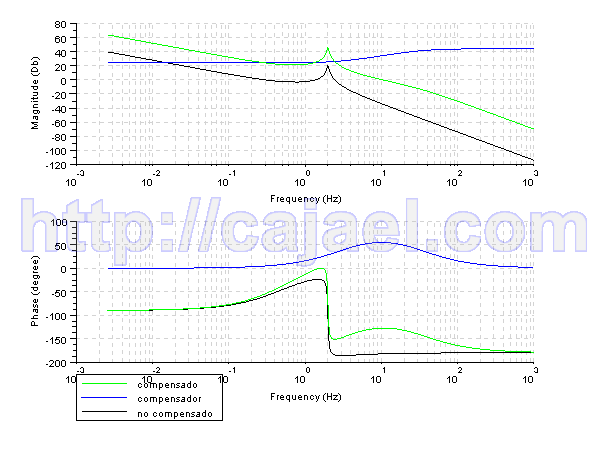
clf;
bode([gbs;gcbs;gtbs],['compensado';'compensador';'no compensado'])

Image P1jun2008ssc

 

Tags:

Español

Añadir nuevo comentario

Más información sobre los formatos de texto

Plain text

  • No se permiten etiquetas HTML.
  • Las direcciones de las páginas web y las de correo se convierten en enlaces automáticamente.
  • Saltos automáticos de líneas y de párrafos.
Pin It