Examenes 2009 RI

Solapas principales

Enviado por pichu en Dom, 07/15/2012 - 14:15

1 Examen Regulacion I, 13 de Febrero 2009
- 1.1 Problema 1 (Diagrama de bloques,formula de la ganancia de Mason)
  
  Resolucion de un diagrama de bloques de dos maneras: Por reduccion del diagrama o por la formula de la ganancia de Mason
- 1.2 Problema 2 (Diagrama polar, criterio de estabilidad de Nyquist)
  
  Dada la funcion de tranferencia de un sistema en lazo abierto utilizando el diagrama polar vamos a aplicar el criterio de estabilidad de Nyquist para ver la estabilidad del sistema, comprobaremos la solucion con el Scilab (plot, real, imag, mtlb_axis, xgrid, roots)
- 1.3 Problema 4 (Lugar de las raices)
  
  Vamos a calcular el lugar de las raices de un sistema, comprobaremos la solucion con el Scilab (evans, mtlb_axis, xgrid, roots)
2 Examen Regulacion I, 30 de Enero del 2009
- 2.1 Ejercicio 1
  
  Vamos a calcular la transformada inversa de Laplace de una funcion de tranferencia, comprobaremos la solucion con el Scilab (tf2ss, pfss, csim, impulse, clf, subplot, plot, xgrid)
- 2.2 Ejercicio 2
  
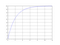  Vamos a calcular la transformada de Laplace y la funcion con respecto al tiempo conociendo el valor de la salida para un tiempo determinado, comprobaremos la solucion con el Scilab (csim, step, clf, plot, xgrid)
- 2.3 Ejercicio 3
  
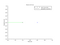  Vamos a calcular el lugar de las raices de un sistema, comprobaremos la solucion con el Scilab (evans, mtlb_axis, plot)
- 2.4 Ejercicio 4 (Criterio de estabilidad de Routh)
  
  Vamos a ver la estabilidad del sistema y donde estan las raices cuando el sistema es marginalmente estable dada la funcion de tranferencia en lazo abierto utilizando: Criterio de estabilidad de Routh; Criterio de Nyquist para un diagrama polar inverso; Criterio de Nyquist; Lugar de las raices. Comprobaremos la solucion con el Scilab (nyquist, xgrid, horner, plot, roots, pdiv, evans, mtlb_axis)