Mensaje de error

  • Deprecated function: The each() function is deprecated. This message will be suppressed on further calls en book_prev() (línea 775 de /home1/montes/public_html/drupal/modules/book/book.module).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Notice: Trying to access array offset on value of type int en element_children() (línea 6422 de /home1/montes/public_html/drupal/includes/common.inc).
  • Deprecated function: implode(): Passing glue string after array is deprecated. Swap the parameters en drupal_get_feeds() (línea 394 de /home1/montes/public_html/drupal/includes/common.inc).

Ejercicio 8.7 Hambley (Respuesta en Frecuencia, Efecto Miller)

Solapas principales

Enviado por pichu en Vie, 08/17/2012 - 21:44

a) Carga igual a 2k

Solucion:

\\begin{displaymath}A_{vo}=-1000\\end{displaymath}


\\begin{displaymath}R_{o}=1\\,k\\Omega\\end{displaymath}


\\begin{displaymath}R_{i}=1\\,M\\Omega\\end{displaymath}


\\begin{displaymath}R_{L}=2\\,k\\Omega\\end{displaymath}


\\begin{displaymath}R_{f}=1\\,M\\Omega\\end{displaymath}


Suponemos que Av va ha ser grande.

\\begin{displaymath}R_{o_{Miller}}=\\frac{R_{f}\\,A_{v}}{A_{v}-1}\\approx R_{f}=1\\,M\\Omega\\end{displaymath}


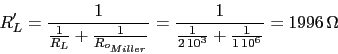
\\begin{displaymath}R''_{L}=\\frac{1}{\\frac{1}{R_{L}}+\\frac{1}{R_{o_{Miller}}}}=\\frac{1}{\\frac{1}{2\\,10^3}+\\frac{1}{1\\,10^6}}=1996\\,\\Omega\\end{displaymath}


\\begin{displaymath}A_{v}=A_{vo}\\,\\frac{R''_{L}}{R''_{L}+R_{o}}=-666.22\\end{displaymath}


\\begin{displaymath}R_{i_{Miller}}=\\frac{R_{f}}{1-A_{v}}=1498.75\\,\\Omega\\end{displaymath}


b) Carga en circuito abierto

Solucion:

\\begin{displaymath}A_{vo}=-1000\\end{displaymath}


\\begin{displaymath}R_{o}=1\\,k\\Omega\\end{displaymath}


\\begin{displaymath}R_{i}=1\\,M\\Omega\\end{displaymath}


\\begin{displaymath}R_{f}=1\\,M\\Omega\\end{displaymath}


Suponemos que Av va ha ser grande.

\\begin{displaymath}R_{o_{Miller}}=\\frac{R_{f}\\,A_{v}}{A_{v}-1}\\approx R_{f}=1\\,M\\Omega\\end{displaymath}


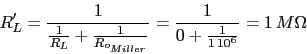
\\begin{displaymath}R''_{L}=\\frac{1}{\\frac{1}{R_{L}}+\\frac{1}{R_{o_{Miller}}}}=\\frac{1}{0+\\frac{1}{1\\,10^6}}=1\\,M\\Omega\\end{displaymath}


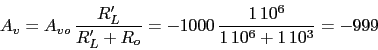
\\begin{displaymath}A_{v}=A_{vo}\\,\\frac{R''_{L}}{R''_{L}+R_{o}}=-1000\\,\\frac{1\\,10^6}{1\\,10^6+1\\,10^3}=-999\\end{displaymath}


\\begin{displaymath}R_{i_{Miller}}=\\frac{R_{f}}{1-A_{v}}=\\frac{1\\,10^6}{1+999}=999.99\\,\\Omega \\end{displaymath}



 

 

Tags:

Español

Añadir nuevo comentario

Más información sobre los formatos de texto

Plain text

  • No se permiten etiquetas HTML.
  • Las direcciones de las páginas web y las de correo se convierten en enlaces automáticamente.
  • Saltos automáticos de líneas y de párrafos.
Pin It