[adsense:responsibe:9545213979]
Apartada b) de la cuestion 3 EDiferenciales 1209S1 (Sistemas de ecuaciones diferenciales lineales homogeneos con coeficientes constantes, solucion particular)
Solapas principales
[adsense:336x280:9156825571]
b) Resolucion:
Vamos a calcular la solucion particular que satisface la condicion del sistema de ecuaciones es:
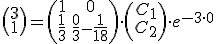
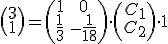
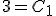
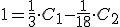
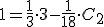
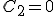
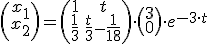
Programa en Sagemath para comprobar el resultado para la solucion particular del sistema de ecuaciones diferenciales lineales homogeneas.
Sage: var('t C1 C2')
Sage: A = matrix([[3, -18], [2, -9]])
Sage: V=matrix([[0],[-1/18]])
Sage: U=matrix([[1],[1/3]])
Sage: SC=matrix([[C1],[C2]])
Sage: X1=U*e^(-3*t)
Sage: X2=U*t*e^(-3*t)+V*e^(-3*t)
Sage: M1=X1.augment(X2)
Sage: dM=M1.determinant()
Sage: R=M1*SC
Sage: R(t=0,C1=3,C2=0)
Resolucion
[3]
[1]
Español
google+:



Añadir nuevo comentario